|
| |
| Autor | Poruka |
|---|
katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Matematičko carstvo Naslov: Matematičko carstvo  Pet 28 Dec - 11:40 Pet 28 Dec - 11:40 | |
| Круг је геометриjскa фигура у равни које се састоји од свих тачака које су подједнако удаљене од једне фиксне тачке и свих тачака које се налазе у унутрашњој области тих тачака. КРУЖНИЦА је скуп тачака у равни једнако удаљених од једне фиксне тачке. Удаљеност сваке тачке на кружници од центра кружнице називамо ПОЛУПРЕЧНИКОМ и означавамо са словом r. Дуж која спаја било које двије тачке на кружници и пролази кроз центар назива се ПРЕЧНИК, и означавамо га са словом R. Дио кружнице између било које двије тачке назива се КРУЖНИ ЛУК. ПОВРШИНА КРУГА: Површина круга једнака је производу квадрата његовог полупречника и броја π,односно:  Круг 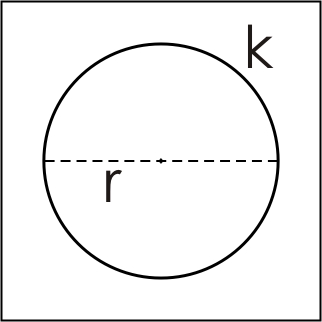 ОБИМ КРУГА: Обим круга једнак је двоструком производу његовог полупречника и броја π, односно: 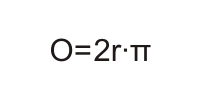  Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pet 28 Dec - 11:42 Pet 28 Dec - 11:42 | |
| Лопта је геометријско тијело у простору које се састоји од свих тачака у простору које су подједнако удаљене од једне фиксне тачке (ЦЕНТАР ЛОПТЕ). Дуж која спаја двије било коју тачку на лопти и центар лопте назива се ПОЛУПРЕЧНИК ЛОПТЕ(означава се са r). ПОВРШИНА ЛОПТЕ: Површина лопте једнака је четверострукој површини њеног великог круга,односно: 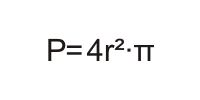 ЗАПРЕМИНА ЛОПТЕ: Запремина лопте једнака је трећини производа њене површине и порупречника,односно:   Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pet 28 Dec - 11:45 Pet 28 Dec - 11:45 | |
| Ваљак је геометријско тијело у простору које је ограничено са два међусобно паралелна и подударна круга и дијелом цилиндричне површи коју описује права која се креће по кружници.  Покретна права назива се ИЗВОДНИЦА, а стална кружница је ВОДИЉА цилиндричне површи. ПОВРШИНА ВАЉКА: Површина ваљка је збир површина база и површине омотача, односно:  ЗАПРЕМИНА ВАЉКА: Запремина ваљка једнака је производу површине основе и висине, односно:   Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pet 28 Dec - 11:47 Pet 28 Dec - 11:47 | |
| Купа је геометријско тијело у простору ограничено са једним кругом (база или основа купе) и једним дијелом обртне конусне површи коју описује полуправа која клизи по наведеном кругу (кружници).  Круг представља ОСНОВУ (БАЗУ) купе, а дио конусне површи представља ОМОТАЧ КУПЕ. Дуж која је нормална на базу, чије су крајње тачке врх купе и центар основе назива се ВИСИНА КУПЕ. ПОВРШИНА КУПЕ: Површина купе једнака је збиру површина основе и омотача, односно:  ЗАПРЕМИНА KУПЕ: Запремина купе једнака је трећини производа површине основе и висине, односно:   Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pet 28 Dec - 11:49 Pet 28 Dec - 11:49 | |
| Призма је геометријско тијело у простору ограничено са два међусобно паралелна и подударна многоугла и онолико паралелограма колико страница има један од тих многоуглова.  Могоуглове називамо ОСНОВЕ или БАЗЕ призме, а паралелограми су БОЧНЕ СТРАНЕ ПРИЗМЕ које чине ОМОТАЧ ПРИЗМЕ. Дуж која је нормална на основе призме и чије крајње тачке припадају равнима основа призме назива се ВИСИНА ПРИЗМЕ (означавамо је са H). Странице многоуглова су ИВИЦЕ призме. Оне које припадају основама су ОСНОВНЕ ИВИЦЕ, а остале су БОЧНЕ ИВИЦЕ. Дуж чије су крајње тачке два тјемена која не припадају истој страни призме, назива се ДИЈАГОНАЛА ПРИЗМЕ (најчешће је означавамо са D). Пресјек призме и равни којој припадају једна ивица и дијагонала призме назива се ДИЈАГОНАЛНИ ПРЕСЈЕК ПРИЗМЕ. Призме према броју страна базе могу бити: тростране, четверостране, петостране, шесто-стране..., n-to стране призме. Ако су основе призме правилни многоуглови, призма се назива ПРАВИЛНА. Призма чија је база паралелограм, назива се ПАРАЛЕЛОПИПЕД. Прав паралелопипед чија је основа правоугаоник, назива се КВАДАР. Онај квадар чије су основне и бочне ивице једнаке, назива се КОЦКА. ПОВРШИНА ПРИЗМЕ: Површина призме је збир површина база и површине омотача, односно:  ЗАПРЕМИНА ПРИЗМЕ: Запремина призме једнака је производу површине основе и висине, односно:   Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pet 28 Dec - 11:51 Pet 28 Dec - 11:51 | |
| Пирамида је геометријско тијело у простору ограничено са једним многоуглом и онолико троуглова колико тај многоугао има страница. Многоугао представља ОСНОВУ или БАЗУ ПИРАМИДЕ, а троуглови чине ОМОТАЧ ПИРАМИДЕ.  Дуж нормална на основу пирамиде, чија је једна крајња тачка врх пирамиде, а друга припада равни основе, назива се ВИСИНА ПИРАМИДЕ(означаваћемо је са H). Према броју страница основе разликујемо тростране, четверостране, петостране, шесто-стране..., n-to стране пирамиде. Ако је база пирамиде правилан многоугао и ако се подножје њене висине налази у центру описане кружнице око основе, онда је пирамида ПРАВИЛНА. Висина бочне стране правилне пирамиде назива се АПОТЕМА. ПОВРШИНА ПИРАМИДЕ: Површина пирамиде једнака је збиру површине основе и површине омотача, односно:  ЗАПРЕМИНА ПИРАМИДЕ: Запреима пирамиде једнака је трећини производа површине основе и висине, односно:   Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pet 28 Dec - 12:01 Pet 28 Dec - 12:01 | |
| Тела ограничена само равним површинама називају се РОГЉАСТА ТЕЛА. Таква тела су: квадар, коцка и многа друга. Тела ограничена само кривим, или кривим и равним површинама, називају се ОБЛА ТЕЛА. Таква тела су: ваљак, купа, лопта. КВАДАР 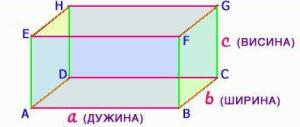 Квадар је геометријско тело ограничено са 6 страна – то су три пара међусобно подударних и паралелних правоугаоника. Квадар има 8 темена - A, B, C, D, E, F, G, H. Квадар има 12 ивица, међу којима уочавамо три групе по 4 једнаке ивице. Њихове дужине означавамо најчешће са а, b и c, а називамо их дужина, ширина и висина. МРЕЖА КВАДРА  Кутија са чајним врећицама је модел квадра.  Отворимо је и разрежимо по неким ивицама. Положимо је на сто. Добили смо мрежу квадра. Мрежа квадра састоји се од 6 правоугаоника. Уочавамо три пара једнаких правоугаоника. Обојимо једнаке правоугаонике.  Сада можемо рачунати површину квадра. ПОВРШИНА КВАДРА 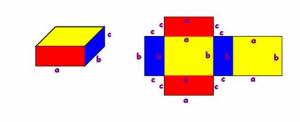 Површина квадра ивица a, b и c једнака је збиру површина његових страна. Како се ради о три пара подударних правоугаоника, то је површина квадра:  КОЦКА  Коцка је квадар чије су све ивице једнаке. Стране коцке су подударни квадрати. МРЕЖА КОЦКЕ 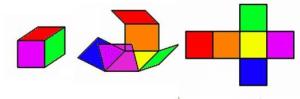 ПОВРШИНА КОЦКЕ Површина коцке ивице а једнака је збиру површина 6 квадрата који је ограничавају.    Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pet 28 Dec - 12:08 Pet 28 Dec - 12:08 | |
| Geometrijska tela priredila: Sanja Jović Geometrijska tela - razni poliedri, lopte, kupe i druga, vekovima su zbunjivali matematičare kroz istoriju zbog svoje trodimenzionalnosti i kompleksnosti. Najveću skupinu geometrijskih tela čine poliedri, ali postoji samo 5 vrsta pravilnih poliedara. To su tetraedar (sa 4 strane), kocka (sa 6 strana), oktaedar (sa 8 strana), dodekaedar (sa 12 strana) i ikosaedar (sa 20 strana). Strane ovih tela najčešće su trouglovi, a mogu biti i kvadrati (kod kocke) i petougaonici (kod dodekaedra). Razne vrste poliedara poređani po broju svojih strana  Pravilni poliedri  Tetraedar (4 strane)  Kocka (6 strana)  Oktaedar (8 strana)  Dodekaedar (12 strana)  Ikosaedar (20 strana)  Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pet 28 Dec - 12:11 Pet 28 Dec - 12:11 | |
| Geometrija
Geometrija je grana matematike koja se bavi proučavanjem likova u ravnini i tela u prostoru.
Danas kada pomislimo na geometriju ona nas odmah asocira na tačke, krugove, trouglove, prave i dr...
Medjutim sama reč geometrija potiče iz drevnih vremena (još u vreme starih Egipćana) i njen prevod bi u bukvalnom smislu bio zemljomerstvo.Da bi se shvatila sama suština geometrije, njen značaj i doprinos razvoju nauke uopšte, ne samo matematike, neophodno je osvrnuti se na istorijski razvoj geometrije.
Sami pojmovi trougao, četvorougao, mnogougao koristili su se u vreme starih Egipćana, Vavilonaca, Sumerana i dr.
Prema pisanim dokumentima, zemljomerstvo je nastalo u Egiptu, jer je bilo neophodno posle poplave Nila meriti imanja i oznacavati medje.Prirodna ljudska radoznalost i istrazivacki duh su doveli do otkrivanja i drgih osobina geometrijskih figura. U pocetku se do opštih osobina dolazilo na osnovu nekoliko eksperimenata, posmatranjem i intuicijom. Ovakav način izvodjenja zaključaka je tzv. nepotpuna indukcija. Negde u 6. Veku pre nove ere Grci su preuzeli vodeću ulogu u razvoju nauke i kulture. Oni su od Egipćana i Vavilonaca preuzeli naučna saznanja, a onda su počeli sve to da sredjuju. Saznanja se prvjeravaju (dokazuju), oslanjajući se na nove usvojene zaključke. Tako nastaje nova metoda zaključivanja, koja ce bitno uticati i na razvoj drugih naučnih oblasti. To je tzv. deduktivna metoda, cija je osnovna karakteristika da sve nove zaključke izvodimo iz ranije utvrdjenih zaključaka - svako novo tvrdjenje se dokazuje.
E sada da predjemo na glavni deo geometrije (geometrijske figure i geometrijska tela).
Geometrijske figure
Geometrijske figure bi najjednostavnije opiso kao objekte u 2D.
Dakle to su objekti u dvodimenzionalnom prostoru.
U sledećem tekstu daću podelu geometrijskih figura i ukratki opis svake figure pojedinačno
Mnogougao
-Trougao
a) pravougli
b) jednakokraki
c) jednakostranični
d) nejednakostranični
-četvorougao
a) deltoid
b) kvadrat
c) paralelogram
d) romb
e) pravougaonik
f) trapez (pravougli,jednakokraki)
-šestougao (pravilni šestougao)
Krug  Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pet 28 Dec - 12:16 Pet 28 Dec - 12:16 | |
|  Krug je geometrijska figura kod koje su sve tacke na kružnici podjednako udaljene od centra kruga. To rastojanje se naziva poluprečnik kruga. Dužina obima kruga jednaka je proizvodu njegovok prečnika I broja (pi = 3.14). Površina kruga jednaka je proizvodu broja pi I kvadrata poluprečnika. Kružni isečak je deo kružne površi ograničem poluprečnicima OA, OB I ukom l. Dva koncentrična kruga koja pripadaju istoj ravni I čiji su poluprečnici r1 i r2 ograničavaju deo kružne površi koja se naziva kružni prsten. Površina kružnog prstena jednaka je razlici površina njegovih krugova. Centralni i periferijski ugao kruga Ugao čije je teme centar kruga naziva se centralni ugao. Svaki ugao čije teme pripada nekoj kružnici, a kraci sadrže tetive te kružnice, naziva se periferijski ugao. Centralni ugao je dobio naziv po tome što mu je teme centar kruga, a kraci sum u poluprečnici. Periferijski ugao jednak je polovini centralnog ugla nad istim lukom. Periferijski uglovi nad istim lukom (tetivom) u istom krugu su jednaki. Ugao koji obrazuje tangenta kruga sa tetivom istog kruga, čija je jedna krajnja tačka dodirna tačka tangente, jednak je periferijskom uglu nad tom tetivom, čije teme leži u oblasti posmatranog ugla. Tetivni mnogougao je mnogougao oko koga se može opisati kružnica, a tangentni mnogougao je mnogougao u koji se može upisati kružnica.  Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pet 28 Dec - 12:21 Pet 28 Dec - 12:21 | |
| Geometrijska tela
Geometrijska tela su objekti u 3D prostoru. Dakle sem površine poseduju i zapreminu.Postoje obruta tela i poliedri kao dve vrste geometrijskih tela.
Obrnuta tela
Valjak – Valjak je geometrijsko telo ograniceno sa dva kruga u paralelnim ravnima I delom cilindricne povrsi, cije su izvodnice normalne na ravni tih krugova.
Krugovi su osnove valjka.
Omotac valjka naziva se deo cilindricne povrsi izmedju ravni osnova.
Visina valjka je duz normalna na osnove, sa krajnjim tackama u osnovama I najcesce se obelezava sa H.
Presek valjka I ravni kojoj pripada osa valjka naziva se osni presek valjka.
Povrsina valjka jednaka je zbiru povrsina osnova I povrsine omotaca.
Zapremina valjka jednaka je proizvodu povrsine njegove osnove I visine.
Kupa – Kupa je geometrijsko telo ograniceno jednim delom obrtne konusne povrsi I krugom.
Krug je osnova kupe.
Omotac kupe je deo konusne povrsi, a vrh konusne povrsi je ujedno I vrh kupe.
Normalna duz na osnovu, cije su krajnje tacke vrh kupe I centar osnove, naziva se visina H.
Odsecak izvodnice konusne povrsi od vrha S do osnove kupe naziva se izvodnica kupe. Takodje izvodnicom cemo nazivati I duzinu tog odsecka.
Sve izvodnice prave kupe su jednake.
Ako ortogonalna projekcija vrha kupe na raven njene osnove ne pada u centar njene osnove onda je to kosa kupa.
Povrsina kupe jednaka je zbiru povrsina osnove I omotaca.
Zapremina kupe jednaka je trecini proizvoda povrsine osnove I visine.
Lopta – Skup svih tacaka u prostoru jednako udaljenih od jedne tacke 0 prostora obrazuje povrs koja se naziva sfera.
Tacka 0 je centar sfere, a duz cije su krajnje tacke centar sfere I proizvoljna tacka na sferi nazivamo poluprecnik.
Duz koja spaja dve tacke na sferi I sadrzi centar sfere je precnik sfere.
Lopta je geometrijsko telo ograniceno sferom.
Centar sfere je ujedno I centar lopte, a poluprecnik sfere je takodje, istovremeno I poluprecnik lopte.
Dakle, skup svih tacaka unutrasnje oblasti sfere I svih tacaka sfere obrazuje loptu.
Lopta je odredjena svojim centrom I poluprecnikom.
Presek lopte I ravni je uvek krug. Ako toj ravni pripada centar lopte, preseceni krug se naziva veliku krug lopte.
Deo lopte koji odseca neka raven naziva se loptin isecak.
Deo sfere, koji zajedno sa osnovom loptinog isecka ogranicava taj odsecak naziva se kalota.
Kalota ciji je granicni krug veliki krug sfere naziva se polusfera, a loptin odsecak cija je osnova veliki krug lopte je polulopta.
Povrsina lopte jednaka je cetvorostrukoj povrsini njenog velikog kruga.
Zapremina lopte jednaka je trecini proizvoda njene povrsine I poluprecnika
M - omotac
P – povrsina
V – zapremina
B – povrsina osnove (baze)
R – precnik
R – poluprecnik
Poliedri
Pravilni poliedar je poliedar sa svim jednakim stranama (dodekaeder, ikosaeder, kocka, oktaeder, tetraeder)
Dodekaeder je pravilni poliedar sa 12 strana.
Ikosaeder je pravilni poliedar sa 20 strana.
Kocka je pravilni poliedar sa 6 strana.
Oktaederje pravilni poliedar sa 8 strana.
Tetraeder je pravilni poliedar sa 4 strane.
Prizma – Prizma je geometrijsko telo ogranicena sa dva paralelna I podudarna mnogougla I onoliko paralelograma koliko stranica ima jedan od tih mnogouglova.
Prizma može biti pravilna trostrana, pravilna šestostrana I pravilna četvorostrana.
Pravilna trostrana prizma je ona kod koje je bazis jednakostranični trougao.
Pravilna četvorostrana prizma je ona kod koje je bazis kvadrat.
Pravilna šestostrana prizma je ona kod koje je bazis pravilni šestougao.
Kvadar je prizma čiji je bazis pravougaonik.
Mnogouglove nazivamo osnove – baze prizme, a paralelogrami su bocne strane prizme. Bocne strane prizme obrazuju omotac prizme.
Visina prizme je duz koja je normalna na osnove prizme I cije krajnje tacke pripadaju ravnima osnova prizmi. Visinu najcesce obelezavamo sa H.
Ivice prizme su stranice mnogouglova.
One koje pripadaju osnovama nazivaju se osnovne ivice, a ostale ivice su bocne ivice prizme.
Dijagonala prizme je duz cije su krajnje tacke dva temena koja ne pripadaju istoj strain prizme. Dijagonalu prizme najcesce obelezavamo sa D.
Presek prizme I ravni kojoj pripadaju jedna ivica I dijagonala prizme naziva se dijagonalni presek prizme.
Povrsina prizme je zbir povrsina osnova I povrsina omotaca.
Zapremina prizme jednaka je prozivodu povrsine osnova I visine.
Prizma moze biti prava I kosa.
Prizma je prava ukoliko su bocne ivice prizme normalne na osnove prizme.
Ukoliko prizma nije prava kaze se da je kosa.
Piramida – Piramida je geometrijsko telo ograniceno delom jedne rogljaste povrsi I jednim mnogouglom.
Teme roglja S je vrh piramide.
Piramida može biti pravilna trostrana, pravilna četvorostrana I pravilna šestostrana.
Pravilna trostrana piramida je ona kod koje je bazis jednakostranični trougao.
Pravilna četvorostrana piramida je ona kod koje je bazis kvadrat.
Pravilna šestostrana piramida je ona kod koje je bazis pravilni šestougao.
Mnogougao koji pripada presecenoj ravni je osnova piramide, a stranice tog mnogougla su osnovne ivice piramide.
Odsecci ivica roglja su bocne ivice piramide a trouglovi odredjeni stranama roglja su bocne strane piramide.
Bocne strane piramide cine omotac piramide. Omotac piramide se najcesce obelezava sa M.
Duz normalna na osnovu piramide, cija je jedna krajnja tacka vrh piramide, a druga pripada ravni osnove, naziva se visina piramide I oznacava se sa H.
Prema broju stranica osnove razlikujemo trostrane, cetvorostrane, petostrane I dr…n-tostrane piramide.
Piramida je pravilna ako je njena osnova pravilan mnogougao I ako se podnozje njene visine poklapa sa centrom opisane kruznice oko osnove.
Kod pravilne piramide bocne strane su podudarni jednakokraki trouglovi.
Visina bocne strane pravilne piramide naziva se apotema.
Apoteme kod pravilnih piramida su jednake.
Povrsina piramide jednaka je zbiru povrsine osnove I povrsine omotaca.
Zapremina piramide jednaka je trecini proizvoda povrsine osnove o visine.  Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Ned 17 Feb - 23:40 Ned 17 Feb - 23:40 | |
| Многоугао је унија скупа тачака затворене просте изломљене линије у равни и скупа тачака одговарајуће унутрашње области. Многоугао коме су све странице и сви углови једнаки назива се ПРАВИЛНИ МНОГОУГАО. Кружница коме припадају сва тјемена једног монгоугла назива се ОПИСАНА КРУЖНИЦА тог многоугла. Кружница која додирује све странице једног многоугла назива се УПИСАНА КРУЖНИЦА тог многоугла. Угао чије је тјеме у центру правилног многоугла, а краци му пролазе кроз два сусједна тјемена многоугла, јесте ЦЕНТРАЛНИ УГАО многоугла, и означава се са α. ПОВРШИНА ПРАВИЛНИХ МНОГОУГЛОВА : Површина правилних многоуглова једнака је половини производа броја њихових страница, полупречника уписаног круга и дужине њихове странице, односно: 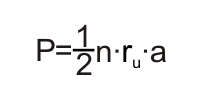 Квадрат 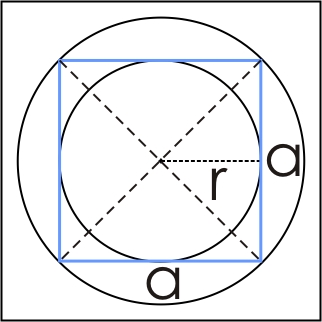 Квадрат Правилни шестоугао 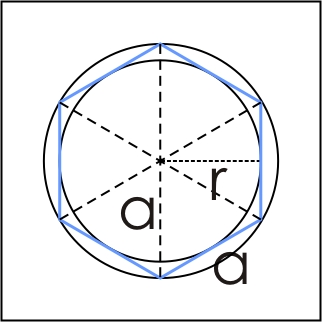 Правилни шестоугао ОБИМ ПРАВИЛНИХ МНОГОУГЛОВА: Обим правилних многоуглова једнак је производу броја њихових страница и дужине странице, односно:   Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | Enigma
MODERATOR


Poruka : 55658
Lokacija : misterija
Učlanjen : 29.03.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pon 22 Apr - 18:49 Pon 22 Apr - 18:49 | |
| UGLOVI
Ugaona linija je unija dve poluprave koje imaju zajedničku početnu tačku.
Svaka ugaona linija ima krake i teme.
Kraci ugaone linije su poluprave koje je zatvaraju, a teme ugaone linije je zajednička tačka iz koje one polaze.
Svaka ugaona linija određuje dva ugla, od kojih je jedan konveksan, a drugi nekonveksan ugao. Svaki konveksni ugao je manji od bilo kog nekonveksnog ugla.
Jedinica za ugao je stepen (0).
Svi konveksni uglovi se dele na:
oštre,
tupe i
prave uglove.
Prav ugao je ugao koji ima 900 .
Oštar ugao je ugao manji od pravog ugla.
Tup ugao je ugao veći od pravog ugla.
Ako se dve poluprave nalaze na istoj pravoj, onda one određuju dva ugla koja su jednaka. Ovi uglovi se nazivaju opružni uglovi.
Opružni ugao je ugao koji ima 180'. On je jednak zbiru dva prava ugla.
Pun ugao je ugao koji ima 360'. On je jednak zbiru dva opružna ugla.
Uglovi koji nastaju presekom dve prave u istoj ravni nazivaju se:
susedni i
unakrsni uglovi.
Unakrsni uglovi su parovi jednakih uglova među uglovima koje su obrazovale prave koje se seku.
Susedni uglovi su dva nadovezana ugla koji imaju zajedničko teme i jedan krak.
Uporedni uglovi su susedni uglovi čiji je zbir jednak opružnom uglu.
Suplementni uglovi su uglovi čiji zbir iznosi 180'.
Komplementni uglovi su uglovi čiji zbir iznosi 90'.
ZAPAMTI
Komplementni uglovi su uvek oštri uglovi.
Svi pravi uglovi su međusobno podudarni.
Svi opružni uglovi su međusobno podudarni.
Konveksni uglovi su manji, a nekonveksni veći od opružnog ugla.
U pravouglom trouglu oštri uglovi su uvek komplementni.
Suplement pravog ugla je prav ugao
Svi komplementni i suplementni uglovi su konveksni.  |
|   | | Enigma
MODERATOR


Poruka : 55658
Lokacija : misterija
Učlanjen : 29.03.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pon 22 Apr - 18:51 Pon 22 Apr - 18:51 | |
| Komplement i suplement su reči latinskog porekla i označavaju dopunu, dodatak nečemu.
Dijametar je reč grškog porekla, a označava nešto što je na drugoj, suprotnoj strani.
Jednakost uglova
Dva ugla su jednaka (podudarna) ako su im odgovarajući kružni lukovi jednakih dužina. Pod odgovarajućim kružnim lukovima smatraju se oni lukovi koji imaju jednake poluprečnike.
Dva ugla koja su oba konveksna ili su oba nekonveksna jednaka su (podudarna) ako su im odgovarajuće tetive jednakih dužina. Pod odgovarajućim tetivama smatraju se one tetive čiji su krajevi podjednako udaljeni od temena uglova.
Kružni luk i tetiva
Svaki ugao čije je teme centar neke kružnice naziva se centralni ugao te kružnice.
Presek kružnice i centralnog ugla kružnice naziva se kružni luk.
Duž koja spaja presečne tačke kružnice i krakova ugla naziva se tetiva.
Tetiva kojoj pripada centar kruga naziva se prečnik ili dijametar kruga.
Prečnik je najduža tetiva kruga. Centralni ugao čija je tetiva prečnik kruga jeste opružni ugao.
boske. |
|   | | Enigma
MODERATOR


Poruka : 55658
Lokacija : misterija
Učlanjen : 29.03.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pon 22 Apr - 19:01 Pon 22 Apr - 19:01 | |
| Kako se izračunava površina geometrijskih figura Kvadrat
Kvadrat je geometrijska figura sastavljena od četiri stranice jednake dužine. Svi uglovi kvadrata su pravi (90'). 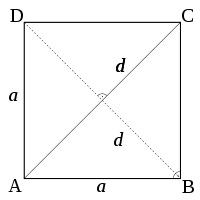 Obim kvadrata O = 4 . a Površina kvadrata P = a . a = a2 a - stranica kvadrata PravougaonikPravougaonik je geometrijska figura sastavljena od četiri stranice, pri čemu su naspramne stranice jednake dužine. Svi uglovi pravougaoika su pravi (90').  Obim pravougaonika O = 2 . (a+b) Površina pravougaonika P = a . b a, b - stranice pravougaonika |
|   | | Enigma
MODERATOR


Poruka : 55658
Lokacija : misterija
Učlanjen : 29.03.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pon 22 Apr - 19:04 Pon 22 Apr - 19:04 | |
| Deljivost brojeva Pojam deljivostiJedan celi broj je deljiv drugim celim brojem ako je ostatak deljenja jednak nuli. Delilac nekog broja jeste svaki prirodni broj kojim je taj broj deljiv. Svaki prirodni broj veći od broja 1 ima bar dva delioca. Sadržilac nekog broja je svaki prirodni broj koji je deljiv tim brojem. Najmanji sadržilac svakog prirodnog broja jeste sam taj broj, a njegov najveći sadržilac ne postoji. Proizvod dva broja deljiv je nekim brojem ako je jedan od činilaca deljiv tim brojem. Zbir dva broja deljiv je nekim brojem samo ako su oba sabirka deljiva tim brojem. Razlika dva broja deljiva je nekim brojem samo ako su i umanjilac i umanjenik deljivi tim istim brojem. Prirodni brojevi veći od 1 koji imaju samo dva delioca, broj 1 i samog sebe nazivaju se prosti brojevi. Prirodni brojevi veći od 1 koji imaju više od dva delioca nazivaju se složeni brojevi. Broj 1 nije ni prost ni složen broj. On je deljiv samo sa sobom. Broj 0 je deljiv bilo kojim prirodnim brojem. DELJIVOST BROJEVA Deljivost brojem 2 Broj je deljiv brojem 2 samo ako mu je poslednja cifra paran broj (0, 2, 4, 6,  Deljivost brojem 3 Broj je deljiv brojem 3 samo ako mu je zbir cifara deljiv brojem 3. Deljivost brojem 4 Broj je deljiv brojem 4 samo ako su mu poslednje dve cifre deljive brojem 4. Deljivost brojem 5 Broj je deljiv brojem 5 samo ako se završava sa ciframa 0 ili 5 Deljivost brojem 6 Broj je deljiv brojem 6 samo ako je deljiv brojevima 2 i 3. Deljivost brojem 9 Broj je deljiv brojem 9 samo ako mu je zbir cifara deljiv brojem 9. Deljivost brojem 10 Broj je deljiv brojem 10 samo ako mu je poslednja cifara 0. Deljivost brojem 25 Broj je deljiv brojem 25 samo ako su mu poslednje dve cifre 00, 25, 50 ili 75.  |
|   | | Enigma
MODERATOR


Poruka : 55658
Lokacija : misterija
Učlanjen : 29.03.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pon 22 Apr - 19:06 Pon 22 Apr - 19:06 | |
| Razlomci
Razlomkom izražavamo broj delova neke celine.
Razlomak se zapisuje pomoću dva prirodna broja i razlomačke crte. Prirodni brojevi pomoću kojih se zapisuje razlomak nazivaju se brojilac i imenilac.
Brojilac je deo razlomka koji se piše iznad razlomačke crte. On označava od koliko jednakih delova se sastoji neka celina (broji delove).
Imenilac je deo razlomka koji se piše ispod razlomačke crte. On označava na koliko je jednakih podeljena neka celina (imenuje delove).
Razlomačka crta je simbol deljenja.
Svaki prirodni broj se može zapisati u obliku razlomka, tako što će imenilac biti broj 1, a brojilac sam taj broj.
Pravi razlomci su manji od 1 i njihovi brojioci su manji od imenioca.
Nepravi razlomci su veći od 1 i njihovi brojioci su veći od imenioca.
Mešoviti brojevi su nepravi razlomci zapisani pomoću razlomka i prirodnog broja.
Množenje i deljenje razlomaka
Kad se brojilac i imenilac nekog razlomka pomnožimo istim prirodnim brojem (n>1) kažemo da smo proširili taj razlomak brojem n. Razlomak se može proširiti bilo kojim prirodnim brojem većim od 1.
Kad se brojilac i imenilac nekog razlomka podelimo istim prirodnim brojem (n>1) kažemo da smo skratili taj razlomak brojem n. Razlomak se može skratiti samo brojem koji je zajednićki delilac njegovog brojioca i imenioca. Najveći zajednički delilac brojioca i imenioca nekog razlomka je največi broj kojim se može taj razlomak skratiti.
Razlomci kod kojih su brojioci i imenioci uzajamno prosti brojevi nazivaju se nesvodljivi razlomci. Ovi razlomci se ne mogu skraćivati.
Sabiranje i oduzimanje razlomaka
Razlomci sa jednakim imeniocima se sabiraju tako što se imenilac prepiše, a saberu se brojioci tih razlomaka. Razlomke sa različitim imeniocima proširivanjem dovodimo na razlomke jednakih imenioca, pa ih onda sabiramo kao razlomke jednakih imenioca.
Razlomci sa jednakim imeniocima se oduzimaju tako što se imenilac prepiše, a oduzmu se brojioci tih razlomaka. Razlomke sa različitim imeniocima proširivanjem dovodimo na razlomke jednakih imenioca, pa ih onda oduzimamo kao razlomke jednakih imenioca.
Množenje i deljenje razlomaka
Razlomak se množi prirodnim brojem tako što se imenilac prepiše, a brojilac se pomnoži tim brojem.
Razlomak se deli prirodnim brojem tako što se brojilac prepiše, a imenilac se pomnoži tim brojem.
Proizvod dva razlomka je razlomak čiji je brojilac jednak proizvodu brojilaca ta dva razlomka, a imenilac proizvod imenilaca ta dva razlomka.
Razlomak se deli drugim razlomkom tako što se taj razlomak pomnoži sa recipročnom vrednošću drugog razlomka. Recipročna vrednost razlomka se dobije kada brojilac i imenilac razlomka zamene svoja mesta.  |
|   | | Enigma
MODERATOR


Poruka : 55658
Lokacija : misterija
Učlanjen : 29.03.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pon 22 Apr - 19:07 Pon 22 Apr - 19:07 | |
| Decimalni zapis razlomaka
Razlomci koji u imeniocu imaju dekadne jedinice (10, 100, 1000, 10000...) nazivaju se dekadni razlomci.
Osnovni dekadni razlomci su dekadni razlomci kod kojih je brojilac 1.
Decimalni zapis se sastoji od dva niza cifara koji su odvojeni zarezom. Cifra sa leve strane decimalnog zareza označavaju broj celih koje razlomak sadrži, a cifre sa desne strane zareza označavaju broj osnovnih decimalnih razlomaka koje taj razlomak sadrži (desetih, stotih, hiljaditih delova, itd...). Cifre sa desne strane nazivamo decimale.
Decimalni zapis razlomaka može biti konačan (sadrži konačno mnogo decimala) i beskonačan (sadrži beskonačno mnogo decimala).
Beskonačne decimalne zapise zamenjujemo konačnim decimalnim zapisom koristeći postupak koji se naziva zaokrugljivanje. Pri zaokrugljivanju brojeva pravi se greška, a da bi ona bila što manja koriste se određena pravila.
zaokrugljivanje brojeva
Pravilo 1
Ako je prva cifra koju odbacujemo 0, 1, 2, 3 ili 4, cifre ispred nje se ne menjaju.
Pravilo 2
Ako je prva cifra koju odbacujemo 6, 7, 8 ili 9, poslednja cifra se povećava za 1.
Pravilo 3
Ako je prva cifra koju odbacujemo 5, a iza nje ima još cifara, poslednja cifra se povećava za 1.
Pravilo 4
Ako je prva cifra koju odbacujemo 5, a iza nje nema više cifara razlikujemo dva slučaja:
a) ako je cifra ispred 5 parna ona ostaje nepromenjena
b) ako je cifra ispred 5 neparna ona se povećava za 1.
boske.  |
|   | | Abu Dabi
MODERATOR


Poruka : 130824
Učlanjen : 07.04.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Uto 23 Apr - 1:59 Uto 23 Apr - 1:59 | |
| Prosti brojeviProsti brojevi  ili prim-brojevi su svi prirodni brojevi veći od broja 1, koji su djeljivi bez ostatka samo s brojem 1 i sami sa sobom. |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Uto 23 Apr - 22:33 Uto 23 Apr - 22:33 | |
| Podudarnost trouglova
Dva trougla su podudarna ako imaju jednake odgovarajuće elemente - stranice i uglove.
Ako su stranice jednog trougla a1, b1, c1 i uglovi α1 , β1 , γ1 , a stranice drugog
trougla a2, b2, c2 i uglovi α2 , β2 , γ2 , oni će biti podudarni ako važi sledeće:
a1 = a2 , b1 = b2, c1 = c2 (jednake odgovarajuće stranice)
α1 = α2, β1 = β2, γ1 = γ2 (jednaki odgovarajući uglovi)
Za dokazivanje podudarnosti trougla koriste se osnovna četiri pravila (stava) o podudarnosti trouglova.
Prvo stav o podudarnosti trouglova - SUS
Ako dva trougla imaju jedake po dve odgovarajuće stranice i njima zahvaćen ugao (ugao između tih stranica), tada su ta dva trougla podudarna.
Ovaj stav se kratko naziva SUS (stranica - ugao - stranica)
Drugo stav o podudarnosti trouglova - USU
Ako dva trougla imaju jednaku po jednu stranicu i jednake na njoj nalegle uglove, tada su ti trouglovi podudarni.
Ovaj stav se kratko naziva USU (ugao - stranica - ugao)
Treći stav o podudarnosti trouglova - SSU
Ako su dve stranice i ugao naspram duže od njih jednog trougla jednaki odgovarajućoj stranici i uglu drugog trougla, tada su ti trouglovi podudarni.
Ovaj stav se kratko naziva SSU (stranica - stranica - ugao)
Četvrti stav o podudarnosti trouglova - SSS
Ako su sve tri stranice jednog trougla jednake odgovarajućim stranicama drugog trougla, tada su ti trouglovi podudarni.
Ovaj stav se kratko naziva USU (ugao - stranica - ugao)
Nije važno koji će stav koristiti prilikom dokazivanja podudarnosti trouglova, važno je samo da se iskoriste podaci koji su unapred dati u zadatku uz primenu matematička pravila koja su već ranije dokazana.
ZAPAMTI
Simetrala ugla deli ugao na dva jednaka dela.
Simetrala stranice je normalna na stranicu i deli je na dva jednaka dela.
Normala na neku pravu zaklapa sa tom pravom prav ugao.
Visina na stranicu trougla je normala na tu stranicu.
Težišna linija deli stranicu na dva jednaka dela.
Tangenta na kružnicu je linija koja dodiruje kružnicu u jednoj tački.
Tangenta i poluprečnik kružnice u tački dodira zaklapaju prav ugao.
Tetiva je duž koja spaja dve tačke kružnice.
Najduža tetiva kružnice je prečnik kružnice.
Svi uglovi u kvadratu i pravougaoniku su pravi uglovi.
Dijagonale kvadrata su jednake i međusobno se polove.
Dijagonale pravougaonika su jednake i međusobno se polove.
Udaljenost tačke od pravca se određuje povlačenjem normale iz date
tačke na pravac.
Središna duž (linija) trougla je duž koja je paralelna sa naspramnom
stranicom trougla i dva puta je kraća od nje.  Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 | |   | | Shadow
ADMIN


Poruka : 97443
Lokacija : U svom svetu..
Učlanjen : 28.03.2011
Raspoloženje : Samo
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Ned 8 Sep - 20:37 Ned 8 Sep - 20:37 | |
| Коцка Коцка (грч. hexáedron - тело са шест површина; код нас хексаедар) је један од пет правилних полиедара. Омеђена је са шест квадратних површи спојених тако да образују тело са дванест дужи и осам темена. Коцка је специјалан случај квадра коме су све странице једнаке. 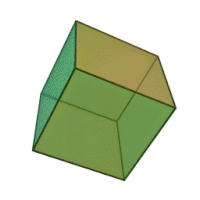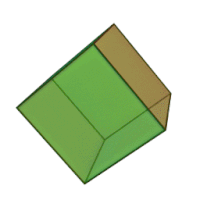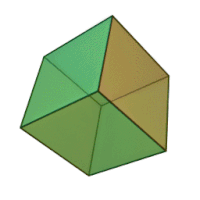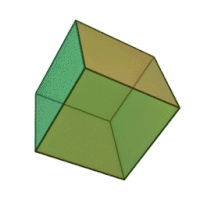 Mreža kocke sastoji iz 6 podudarnih kvadrata, čije su stranice jednake ivici kocke. Ako je P1 površina jednog kvadrata, tada je površina kocke P=6P1=6a2. Mreža kvadra se sastoji iz 6 pravougaonika, od kojih su po dva nesusedna podudarna. Površine tih pravougaonika su P1=a⋅c, P2=a⋅b, P3=b⋅c, a površina kvadra: P=2P1+2P2+2P3 = 2(a⋅b+b⋅c+c⋅a). |
|   | | Shadow
ADMIN


Poruka : 97443
Lokacija : U svom svetu..
Učlanjen : 28.03.2011
Raspoloženje : Samo
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Pon 16 Sep - 21:24 Pon 16 Sep - 21:24 | |
| СКУПОВИ Скуп је основни математички појам који се не дефинише. Он се описује као целина објеката који имају заједничко својство или особину. Обележавају се великим латиничним словима,нпр: A,B,C,D,S,Y… Скуп се може исказати Венеовим дијаграмом. ~Скуп је одређен својим елементима. ~Редослед елемената у скупу није важан. ~N-скуп свих природних бројева N={1,2,3…15,16,17…190,191,192…1200,1201…, 63000000,….} ~Посебно издвајамо празан скуп. Празан скуп је скуп који нема елемената и означава се симболом ∅. ~За скупове А и B кажемо да су једнаки ако имају једнаке елементе и пишемо А=B. Припадност елемената скупу  Ознака: елемент x не припада скупу А Подскуп  За скуп А кажемо да је подскуп скупа B онда и само онда ако је сваки елемент из А уједно и елемент из B. 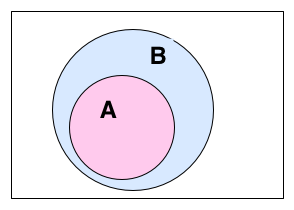 Пресек скупова 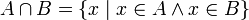 Пресек два скупа је скуп који садржи заједничке елементе оба скупа. За скупове А и B кажемо да су дисјунктни ако и само ако је њихов пресек празан скуп. 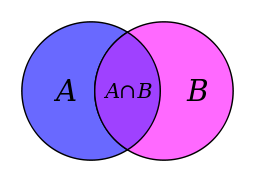 Унија скупова  Унија два скупа је скуп који садржи елементе оба скупа при чему се исти елементи наводе само једном. 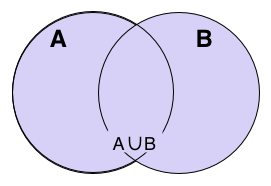 Разлика скупова 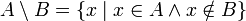 Разлика скупова А и B је скуп који садржи елементе који су у скупу А, а нису у скупуB.  Основна својства скупова: комутативност, асоцијативност, дистрибутивност 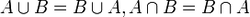 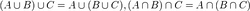  ivanaantic.weebly.com  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Sub 19 Okt - 0:51 Sub 19 Okt - 0:51 | |
| Eratosten  Grčki matematičar, geograf, putopisac i astronom, poznat kao „otac geografije“. Eratosten (276. g.p.n.e. -194. g.p.n.e.),. rođen je u Kireni (danas u Libiji), a umro u ptolomejskoj Aleksandriji. Stekao je slavu kao prvi koji je upoznao sistem širina i dužina, te prvi koji je izračunao Zemljinu veličinu. Eratosten se obrazovao u Aleksandriji i nekoliko godina u Atini. Ptolomej III Euergeta imenovao ga je 236. g.p.n.e. predsednikom Aleksandrijske biblioteke. Eratosten je dao nekoliko važnih doprinosa matematici i nauci. Bio je prijatelj s Arhimedom. Oko 255. g.p.n.e. izumeo je armilarnu sferu, koja se naširoko koristila sve do pronalaska planetorijuma u 18.veku.  Čuveno je Eratostenovo sito kojim se određuju svi prosti brojevi manji od nekog, unapred datog, prirodnog broja : 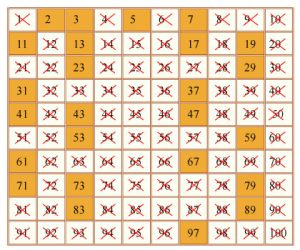 -Napišite sve brojeve od 2 do n -Zaokružite prvi broj na spisku (dvojka) pa precrtajte sa spiska sve brojeve deljive sa dva. -Zaokružite prvi neprecrtani broj sa spiska pa precrtajte sa spiska sve brojeve deljive brojem koji ste poslednji zaodružili. -Ponavite postupak sa sledećim naprecrtanim brojevima sve dok brojevi sa spiska ne budu zaokruženi ili precrtani. Zaokruženi brojevi su traženi prosti brojevi.   Razmisli dva puta pre nego što otvoriš usta Razmisli dva puta pre nego što otvoriš usta  |
|   | | katarina
MODERATOR


Poruka : 74915
Učlanjen : 06.06.2011
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  Uto 10 Dec - 17:12 Uto 10 Dec - 17:12 | |
| |
|   | | Sponsored content
 |  Naslov: Re: Matematičko carstvo Naslov: Re: Matematičko carstvo  | |
| |
|   | | |
Similar topics |  |
|
| Strana 1 od 2 | Idi na stranu : 1, 2  | |
| | Dozvole ovog foruma: | Ne možete odgovarati na teme u ovom forumu
| |
| |
| | Ko je trenutno na forumu | Imamo 358 korisnika na forumu: 0 Registrovanih, 0 Skrivenih i 358 Gosta :: 2 Provajderi
Nema
Najviše korisnika na forumu ikad bilo je 930 dana Pet 27 Sep - 15:38
|
| Dvorana slavnih |
Naj Avatar Haossa !

Kreja
|
| Poslanici naj aktivniji nedelje | |
|