Diferencijalne jednacine

1.1 Razdvojene promenljive






U opštem slučaju:





1.2 Homogena diferencijalna jednačina



Smenom: polazna jednačina postaje:



tj. diferencijalna jednačina oblika.

**Primedba** - Diferencijalna jednačina oblika:



gde je a, b, c, A, B, C = const, može se svesti na jednačinu oblika . Moguća su dva slučaja:

1. Slučaj

Ako je smenom: jednačina postaje:



Sistem jednačina:



ima rešenje po a i b pa jednačina postaje:

a to je jednačina oblika .


2. Slučaj

Neka je , tj. gde je k konstanta. Smenom , gde je u nova nepoznata f-ja promenljive x. Jednačina postaje:

odnosno jednačina oblika .



1.3 Linearna diferencijalna jednačina



Ako je jednačina se naziva homogena linearna diferencijalna jednačina.


1. Slučaj

Homogena jednačina:



za postaje:



tj. jednačina oblika čije je rešenje:



Može se uzeti kao rešenje jednačine.


2. Slučaj

Da bi rešili pretpostavimo :





ako se jn-e i zamene u dobija se:



odnosno:



pa je opšte rešenje jednačine:



U eksplicitnom obliku opšte rešenje jednačine dato je kao:



tj. rešenje je izraženo kao linearna funkcija integracione konstante.



1.4 Bernulijeva jednačina



Gde je , za jednačina postaje linearna.

Uvođenjem smene , gde je z nova nepoznata f-ja a k konstanta, jednačina postaje:





Konstantu k treba izabrati tako da je:



Posle ove smene jednačina glasi:



a to je linearna jednačina. Opšte rešenje ove jednačine ima oblik:



Prema tome, opšte rešenje Bernulijeve jednačine može se izraziti u eksplicitnom obliku:





1.5 Rikartijeva jednačina



Za jednačina postaje Bernulijeva jednačina , odnosno linearna jednačina . U opštem slučaju jednačina se ne može rešiti.

Ako je poznato jedno partikularno rešenje može se dobiti i opšte rešenje jednačine .

Smenom , gde je y1(x) jedno partikularno rešenje a z nova nepoznata funkcija jednačina postaje:





a to je linearna jednačina. Opšte rešenje ove jednačine ima oblik:



Prema tome opšte rešenje Rikartijeve jednačine ima oblik:



gde je C proizvoljna konstanta a F, G, H i K određene funkcije.



1.6 Klerova jednačina



Smenom jednačina postaje:



odakle se, nakon diferenciranja po x, dobija:



1. Slučaj

Ako je pa na osnovu jednačine opšte rešenje jednačine ima oblik:




2. Slučaj

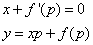
Ako je eliminacijom p iz jednačina dobija se singularno rešenje jednačine koje nije izraženo u opštem rešenju.



1.7 Lagranževa jednačina



Ova jednačina se rešava slično kao i Klerova. Posle smene jednačina dobija oblik:



odakle se, nakon diferenciranja, dobija:





Ako je jednačina je Klerova, pretpostavimo onda da je tada jednačina postaje:



a to je linearna jednačina. Jednačina ima rešenje oblika



pa je opšte rešenje Lagranževe jednačine u parametarskom obliku:





1.8 Jednačina prvog reda drugog stepena



Ako se jednačina može napisati u obliku:



tada se rešavanje jednačine svodi na rešavanje dve jednačine prvog stepena:



Opšta rešenja ovih jednačina su pa je opšte rešenje jednačine :



gde je C proizvoljna konstanta.



1.9 Totalni diferencijal



gde funkcije P i Q imaju neprekidne parcijalne izvode po x i z. Ako postoji funkcija u(x,y) takva da važi:



tada se jednačina naziva jednačina sa totalnim diferencijalom, ili egzaktna diferencijalna jednačina..

Opšte rešenje egzaktne diferencijalne jednačine određeno je relacijom:



gde je C proizvoljna konstanta.

Da bi se odredila funkcija u, za koju važi , treba poći od jednakosti:



odakle se, upoređivanjem sa dobija:



odnosno:




Ovi mešoviti izvodi su po pretpostavci neprekidni pa su i jednaki, pa je, prema tome, potreban uslov da jednačina bude sa totalnim diferencijalom.

Ako je ovaj uslov ispunjen iz prve jednačine u dobija se:



gde je f(y) neprekidna funkcija. Diferenciranjem izraza dobija se:





Druga jednačina u i jednačina daju:



gde je K proizvoljna konstanta.

Konačno se dobija:



pa je opšte rešenje jednačine dato sa:



gde je C proizvoljna konstanta.



svetnauke.org

2.1 Slučaj svođenja na jednačinu prvog reda

Opšta diferencijalna jednačina drugog reda ima oblik:



U nekim slučajevima jednačina može se svesti na diferencijalnu jednačinu prvog reda.

1. Slučaj



Pomoću smene ova jednačina se svodi na jednačinu prvog reda oblika:

.


2. Slučaj



Za rešavanje ovakve jednačine treba koristiti smenu . Tada se dobija . Tada polazna jednačina postaje jednačina prvog reda:

.



2.2 Homogena linearna diferencijalna jednačina drugog reda sa konstantnim koeficijentima



Rešenje jednačine treba tražiti u obliku , gde je l konstanta. Odavde se dobija pa jednačina dobija oblik:





Dakle, je rešenje jednačine ako l zadovoljava tzv. karakterističnu jednačinu .

Moguća su tri slučaja:

1. Slučaj

tada su linearno nezavisna rešenja jednačine pa je opšte rešenje jednačine dato sa:



gde su C1 i C2 proizvoljne konstante.


2. Slučaj

tada je (). Na osnovu prethodnog slučaja rešenje jednačine može se izraziti u obliku:



Pošto je rešenje može se transformisati u sledeći oblik:





gde su A i B proizvoljne konstante.


3. Slučaj

u ovom slučaju partikularna rešenja jednačine su linearno nezavisna pa opšte rešenje glasi:

.



2.3 Nehomogena linearna diferencijalna jednačina drugog reda sa konstantnim koeficijentima



Rešenje odgovarajuće homogene jednačine, oblika , može se uvek odrediti pa se uvek može odrediti i rešenje jednačine . U opštem slučaju za rešavanje ove jednačine koristi se metod varijacije konstanata, ali za neke specijalne oblike funkcije h(x) taj metod se može izbeći:

1. Slučaj



Ako je partikularno rešenje jednačine treba tražiti u obliku polinoma:



Koeficijenti polinoma polinoma dobijaju se metodom neodređenih koeficijenata.

Ako je partikularno rešenje treba tražiti u obliku:



Za rešenje jednačine dobija se direktnom integracijom.


Metod neodređenih koeficijenata

Naći sve izvode rešenja:



Sve dobijene izvode vratiti u jednačinu a zatim izjednačiti koeficijente uz odgovarajuće članove.


2. Slučaj



U zavisnosti od rešenja karakteristične jednačine:



partikularno rešenje treba tražiti u obliku:

(a)

(b)

(c)

gde je K privremeno neodređena konstanta.


3. Slučaj



Ako ip nije koren karakteristične jednačine partikularno rešenje treba tražiti u obliku:



a ako jeste, onda rešenje tražiti u obliku:




4. Slučaj

, gde je Pn(x) polinom n-tog stepena.

Ako a nije rešenje karakteristične jednačine tada je , gde je Qn(x) polinom n-tog stepena sa neodređenim koeficijentima. Ako je a rešenje jednačine onda je , gde je r višestrukost rešenja a
().


5. Slučaj



Ako nije rešenje karakteristične jednačine uzeti:



gde su SN(x) i TN(x) polinomi stepena .

U suprotnom slučaju, ako je rešenje karakteristične jednačine onda je:



gde je r višestrukost rešenja (za jednačine drugog reda ).



2.4 Ojlerova linearna jednačina drugog reda



Prvo treba rešiti odgovarajuću homogenu jednačinu:



Ako se pretpostavi da jednačina ima rešenje oblika ( je parametar koji treba odrediti) tada je pa jednačina postaje:





Razlikuje se nekoliko slučajeva:

1. Slučaj



Opšte rešenje jednačine glasi:



gde su C1 i C2 proizvoljne konstante.


2. Slučaj



U ovom slučaju, iz



dobija se opšte rešenje jednačine u obliku:



gde su A1 i A2 proizvoljne konstante.


3. Slučaj



U ovom slučaju partikularna rešenja jednačine su i pa opšte rešenje glasi:



gde su C1 i C2 proizvoljne konstante.


U sva tri slučaja prećutno je pretpostavljeno da je . Ako je , treba poći od rešenja oblika .

Opšte rešenje nehomogene jednačine dobija se iz opšteg rešenja homogene jednačine standardnim metodom varijacije konstanata.



svetnauke.org