|
| | Zanimljivosti iz matematike |    |
| |
| Autor | Poruka |
|---|
kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Pet 3 Jun - 19:28 Pet 3 Jun - 19:28 | |
| - Citat :
- Geometrija posjeduje dva velika blaga: jedno je Pitagorin poučak, a drugo zlatni rez. Prvo se može usporediti sa čistim zlatom, a drugo s draguljem neprocjenjive vrijednosti.
Johannes Kepler U našem svakodnevnom životu neprestano se susrećemo s matematikom i geometrijom. Svijet koji oblikuje čovjek prepun je pravih kuteva, crta i predmeta pravilnih geometrijskih oblika. Matematika je danas obična, svjetovna znanost, ona je alat kojim se služimo da bismo brojali, računali, mjerili i upravljali svijetom oko sebe. Pritom zaboravljamo ono dublje, metafizičko značenje matematike i geometrije o kojem su govorili mnogi matematičari i filozofi.Pitagora je smatrao da u osnovi svega leži broj i da je čitav svemir jedna matematička struktura. Zato putem geometrije, koja se bavi redom u prostoru kroz mjerenje odnosa među različitim oblicima, možemo istraživati principe koji vladaju u svemiru. Matematički odnosi i brojevi postoje a priori, oni mogu, ali ne moraju imati svoju paralelu u pojavnom svijetu. Cilj je geometrije omogućiti čovjekovoj svijesti da stvori kanal putem kojeg materijalna razina, razina manifestiranih oblika, može poprimiti apstraktne, kozmičke principe.Istražujući odnose među oblicima, matematičari su došli do nekih čudesnih brojeva, poput e, baze prirodnog logaritma, ili π (pi), odnosa opsega kruga i njegova promjera, koji kao da izrastaju iz temeljne strukture kozmosa. Jedan od takvih brojeva je i Φ (phi, fi), zlatni broj, zlatni rez ili zlatni razmjer. Omjer i razmjerZlatni rez se brojčano može izraziti kao konstanta čija veličina iznosi 1.6180339…, ali njegovo značenje nije toliko u njegovoj numeričkoj vrijednosti, koliko u razmjeru koji određuje. Da bismo ovo razumjeli, moramo razjasniti pojmove omjera i razmjera (proporcije). Omjer je odnos dviju mjera, veličina, količina ili dvaju svojstava i izražava se formulom a : b. Tako omjer predstavlja mjeru različitosti, i to različitosti koju može spoznati barem jedno od naših osjetila. Odnos a : b nije samo osnovni pojam za sve aktivnosti opažanja, nego označava i osnovni proces inteligencije gdje simbolizira usporedbu između dviju stvari, što je osnova za stvaranje prosudbi.Proporcija je, međutim, složenija. Razmjer ili proporcija znači jednakost između dvaju odnosa, tj. kada se jedan element prema drugom odnosi kao treći prema četvrtom, a izražava se formulom a : b = c : d. To predstavlja finiju razinu inteligencije od odgovora na jednostavnu različitost odnosa. Stari Grci su to nazivali analogija.Pitagorejci su razlikovali dva tipa analogije. Prvi je definiran prije navedenom formulom i sastoji se od četiriju različitih elemenata. Taj se tip proporcije naziva diskontinuirani. Ali ako se ograničimo na samo tri elementa razmjera, dobit ćemo bitno egzaktniji odnos koji možemo izraziti formulom a : b = b : c.Ovo se naziva kontinuirana proporcija, jer su dva omjera povezana jednim zajedničkim elementom.Međutim, ta tri elementa razmjera možemo reducirati na samo dva. Jedini prirodni aritmetički razmjer koji možemo dobiti sa samo dva elementa izražava se formulom a : b = b : (a + b), gdje se manja veličina prema većoj odnosi kao veća prema zbroju obadviju veličina. Ovaj se razmjer naziva zlatni razmjer.Numerička vrijednost broja Φ je (√5+1)/2 ili približno 1.6180339. Fibonaccijev niz brojeva Uz zlatni broj Φ vezane su mnoge matematičke zanimljivosti. Primjerice, bilo koju potenciju broja Φ možemo dobiti tako da zbrojimo dvije prethodne potencije. Npr. Φ 4 + Φ 5 = Φ 6Fibonaccijev niz brojeva, nazvan po talijanskom matematičaru Leonardu Fibonacciju iz XIII. stoljeća, jedan je od načina na koji možemo generirati Φ. Prva dva člana Fibonaccijeva niza su 1 i 1, a svaki sljedeći član dobije se tako da se zbroje prethodna dva:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…Ako bilo koja dva uzastopna člana međusobno podijelimo, dobit ćemo niz brojeva koji osciliraju oko broja Φ; što je vrijednost članova niza veća, to će vrijednost koju dobijemo njihovim dijeljenjem biti bliža broju Φ. Npr:8 : 5 = 1.6 Uz zlatni broj Φ vezane su mnoge matematičke zanimljivosti. Primjerice, bilo koju potenciju broja Φ možemo dobiti tako da zbrojimo dvije prethodne potencije. Npr. Φ 4 + Φ 5 = Φ 6Fibonaccijev niz brojeva, nazvan po talijanskom matematičaru Leonardu Fibonacciju iz XIII. stoljeća, jedan je od načina na koji možemo generirati Φ. Prva dva člana Fibonaccijeva niza su 1 i 1, a svaki sljedeći član dobije se tako da se zbroje prethodna dva:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…Ako bilo koja dva uzastopna člana međusobno podijelimo, dobit ćemo niz brojeva koji osciliraju oko broja Φ; što je vrijednost članova niza veća, to će vrijednost koju dobijemo njihovim dijeljenjem biti bliža broju Φ. Npr:8 : 5 = 1.6
13 : 8 = 1.625
…
377 : 233 = 1.6180257…
610 : 377 = 1.6180371…Iako Fibonaccijev niz počinje s 1, 1, niz je moguće započeti s bilo koja dva broja. U svakom nizu ovakvog tipa, omjer uzastopnih članova težit će prema Φ.
 Zlatni pravokutnikZlatni pravokutnik je onaj pravokutnik kod kojeg je omjer duže i kraće stranice jednak Φ. Na slici je prikazana geometrijska konstrukcija zlatnog pravokutnika iz kvadrata.1. Odredimo točku E, polovište stranice AB kvadrata ABCD.
2. Povučemo dužinu koja spaja točke C i E.
3. Šestarom povučemo luk sa središtem u točki E i odredimo točku F. Pravokutnik BDGF je zlatni pravokutnik.Ako iz zlatnog pravokutnika izrežemo kvadrat čija je stranica jednaka manjoj stranici pravokutnika, pravokutnik koji nam je preostao također će biti zlatni. Tako je na gornjoj slici i pravokutnik ACFG zlatni.U geometriji se Φ pojavljuje i kod nekih pravilnih geometrijskih likova, npr. kao odnos polumjera kruga i stranice pravilnog deseterokuta oko kojeg je krug opisan, ili kod pentagrama, gdje je svaka dužina podijeljena prema zlatnom rezu. Zlatni rez u prirodiZlatni rez i Fibonaccijevi brojevi pojavljuju se na mnogo mjesta u prirodi, a brojne studije potvrđuju njihovu učestalost. U svijetu prirode rast znači dodavanje određene količine jedinki već postojećima, makar te jedinke bile sitne poput molekule. Čini se da je upravo Φ idealna mjera za rast takve vrste. Dobar je primjer za to prelijepa kućica glavonošca iz roda Nautilus. Ona raste u obliku spirale koja se u svakom krugu povećava razmjerno broju Φ. Grananje kao još jedan oblik prirodnog rasta odvija se prema Fibonaccijevu nizu brojeva. Logaritamska spirala, otkrivena u položaju koji ljudski i životinjski fetus zauzimaju u posteljici, prisutna je i u modelu rasta mnogih biljaka. Raspored sjemenki kod cvijeta suncokreta slijedi logaritamsku spiralu na bazi zlatnog reza. Nadalje, suncokret ima 55 spirala u smjeru kazaljke na satu koje se nalaze preko 34 ili 89 spirala položenih suprotno od smjera kazaljke na satu. Ove brojeve prepoznajemo kao dio Fibonaccijeva niza koji generira broj Φ.Zanimljiv primjer Fibonaccijeva niza u prirodi možemo pronaći kod pčela. Kod njih je jedinstveno da trutovi nastaju iz matičinih neoplođenih jajašaca, tako da imaju samo majku, dok ženske radilice imaju i majku i oca. Ali i kod jednih i kod drugih, ukupan broj pčela svake generacije slijedi Fibonaccijev niz brojeva.Zlatni rez, vezano uz njegovo pojavljivanje kod pentagrama, možemo pronaći kod svakog cvijeta s pet latica. Porodica ruža, kao i cvjetovi svih jestivih voćaka, imaju pet latica ili broj latica koji je višekratnik broja pet. Tradicionalna medicina smatra da kroz taj broj biljke daju čovjeku znak da su jestive. Logaritamska spirala, otkrivena u položaju koji ljudski i životinjski fetus zauzimaju u posteljici, prisutna je i u modelu rasta mnogih biljaka. Raspored sjemenki kod cvijeta suncokreta slijedi logaritamsku spiralu na bazi zlatnog reza. Nadalje, suncokret ima 55 spirala u smjeru kazaljke na satu koje se nalaze preko 34 ili 89 spirala položenih suprotno od smjera kazaljke na satu. Ove brojeve prepoznajemo kao dio Fibonaccijeva niza koji generira broj Φ.Zanimljiv primjer Fibonaccijeva niza u prirodi možemo pronaći kod pčela. Kod njih je jedinstveno da trutovi nastaju iz matičinih neoplođenih jajašaca, tako da imaju samo majku, dok ženske radilice imaju i majku i oca. Ali i kod jednih i kod drugih, ukupan broj pčela svake generacije slijedi Fibonaccijev niz brojeva.Zlatni rez, vezano uz njegovo pojavljivanje kod pentagrama, možemo pronaći kod svakog cvijeta s pet latica. Porodica ruža, kao i cvjetovi svih jestivih voćaka, imaju pet latica ili broj latica koji je višekratnik broja pet. Tradicionalna medicina smatra da kroz taj broj biljke daju čovjeku znak da su jestive. Čovjek i zlatni rezKanon ljudskog tijela, odnosno opis prosječnih i idealnih mjera ljudskog tijela, bio je predmet čovjekova interesa još od najstarijih vremena. Poznati su nam kanoni iz doba faraona, Polikletov, Leonardov, Albertijev, Michelangelov i brojni drugi. U mnogima od njih, ljudsko je tijelo promatrano kao složen sustav odnosa koji se izjednačavaju u zlatnom rezu.Prema egipatskim, grčkim i japanskim kanonima, pupak dijeli čovjekovo tijelo prema zlatnom rezu, dok se spolni organi nalaze točno na polovici čovjekove pune visine. Ovo označava povezanost seksualnosti s funkcijom dualnosti, podjele na dva, tj. reprodukcije. Kod rođenja, međutim, pupak se nalazi na pola visine djetetova tijela i tijekom rasta pomiče se na točku zlatnog reza. To simbolički označava kretanje dualne, spolno podijeljene prirode prema harmoničnijem odnosu koji simbolizira zlatni rez. 
Zlatni rez u umjetnostiOtkako je čovječanstvo počelo razmišljati o geometrijskim oblicima svoga svijeta, brojne prirodne, filozofske i estetske studije bavile su se zlatnim rezom. Zlatni je rez bio prisutan u sakralnoj umjetnosti Egipta, Indije, Kine i drugih drevnih civilizacija. Dominirao je u grčkoj umjetnosti, ostao skriven, ali prisutan u gotičkom srednjem vijeku, da bi ponovno bio slavljen u renesansi.Možda najslavniji primjer primjene zlatnog reza u umjetnosti je Partenon, grčki hram posvećen božici Ateni koji su sagradili arhitekti Iktin i Kalikrat. Kod Partenona je zlatni pravokutnik prisutan i u pročelju i u tlocrtu hrama. Omjeri veličina pojedinih dijelova hrama, sve do najsitnijih, predstavljaju razmjer zlatnog reza. Grčki su umjetnici ovaj princip razumijevali ne samo kao odnos dužina, nego i kao odnos površina, zavladavši na taj način beskrajem lijepih oblika.Analize pojedinih autora pokazuju da je u većini klasičnih građevina na neki način ugrađen zlatni rez. Fidija (Phidias), kipar čija djela krase Partenon, svoje je kipove proporcionirao prema ovom razmjeru. Zato je američki matematičar Mark Barr dvadesetih godina prošlog stoljeća predložio da se numerička vrijednost zlatnog razmjera označi slovom Φ (phi) prema prvom slovu imena čuvenog kipara. Iako se zlatni rez najčešće veže uz grčku umjetnost, on je bio poznat i ranije, još u vrijeme Babilonaca i Egipćana. Grci su od Egipćana preuzeli ideju da pomoću osnovnih geometrijskih likova (kvadrata, kruga i istostraničnog trokuta) te razmjera poput zlatnog reza prenesu principe makrokozmosa u čovjeku bliži svijet mikrokozmosa. Grob Ramzesa IV. u Dolini kraljeva lijep je primjer povezivanja arhitekture i sakralne geometrije. Naime, Ramzes IV. sahranjen je u grobnici uklesanoj u stijeni u trostrukom sarkofagu. Sarkofag u kojem se nalazilo tijelo bio je u obliku dvostrukog kvadrata, a srednji sarkofag bio je u obliku zlatnog pravokutnika. Treći, vanjski sarkofag, sastojao se od dva takva pravokutnika. Geometrijska analiza predmeta pronađenih u grobnicama pokazala je da su i oni oblikovani korištenjem kvadrata i zlatnog reza, što pokazuje prisutnost sakralne geometrije ne samo u velikim arhitektonskim formama, nego i kod najmanjih svetih predmeta.Zlatni rez ne pojavljuje se samo u arhitekturi. Analiza kompozicije slike Krštenja Kristova Piera della Francesce pokazuje nam da je ova slika zapravo geometrijska alegorija principa Svetog Trojstva, pri čemu Sveto Trojstvo slijedi geometrijski simbolizam zlatnog reza. Kristovo tijelo smješteno je unutar površine Iako se zlatni rez najčešće veže uz grčku umjetnost, on je bio poznat i ranije, još u vrijeme Babilonaca i Egipćana. Grci su od Egipćana preuzeli ideju da pomoću osnovnih geometrijskih likova (kvadrata, kruga i istostraničnog trokuta) te razmjera poput zlatnog reza prenesu principe makrokozmosa u čovjeku bliži svijet mikrokozmosa. Grob Ramzesa IV. u Dolini kraljeva lijep je primjer povezivanja arhitekture i sakralne geometrije. Naime, Ramzes IV. sahranjen je u grobnici uklesanoj u stijeni u trostrukom sarkofagu. Sarkofag u kojem se nalazilo tijelo bio je u obliku dvostrukog kvadrata, a srednji sarkofag bio je u obliku zlatnog pravokutnika. Treći, vanjski sarkofag, sastojao se od dva takva pravokutnika. Geometrijska analiza predmeta pronađenih u grobnicama pokazala je da su i oni oblikovani korištenjem kvadrata i zlatnog reza, što pokazuje prisutnost sakralne geometrije ne samo u velikim arhitektonskim formama, nego i kod najmanjih svetih predmeta.Zlatni rez ne pojavljuje se samo u arhitekturi. Analiza kompozicije slike Krštenja Kristova Piera della Francesce pokazuje nam da je ova slika zapravo geometrijska alegorija principa Svetog Trojstva, pri čemu Sveto Trojstvo slijedi geometrijski simbolizam zlatnog reza. Kristovo tijelo smješteno je unutar površine 1 × 1/Φ 3, a njegova visina je 3 × 1/Φ 3. I drugi elementi kompozicije vođeni su sličnim principima, u skladu s kršćanskim simbolizmom, npr. položaj Kristova srca, pupka, ruke Sv. Ivana itd.Na slici Piera della Francesce Krist povezuje geometrijskom, matematičkom logikom pojmove duha i materije, univerzalnog i individualnog, konačnog i beskonačnog. Upravo harmonizacija s onim višim, nama teško dokučivim sferama bila je cilj svih istinskih filozofa. Za mnoge od njih zlatni rez je bio izravna veza s tim sferama, njihova manifestacija u našem nesavršenom pojavnom svijetu. Bilo bi pretjerano reći da se zlatni rez nalazi posvuda u prirodi, ali gdje god opazimo pojavu izuzetne ljepote i sklada, najčešće ćemo otkriti prisutnost zlatnog reza. On je podsjetnik na srodnost našeg pojavnog svijeta s njegovim savršenim izvorom i s njegovom potencijalnom budućom evolucijom.Autor: Suzana Dobrić 1 × 1/Φ 3, a njegova visina je 3 × 1/Φ 3. I drugi elementi kompozicije vođeni su sličnim principima, u skladu s kršćanskim simbolizmom, npr. položaj Kristova srca, pupka, ruke Sv. Ivana itd.Na slici Piera della Francesce Krist povezuje geometrijskom, matematičkom logikom pojmove duha i materije, univerzalnog i individualnog, konačnog i beskonačnog. Upravo harmonizacija s onim višim, nama teško dokučivim sferama bila je cilj svih istinskih filozofa. Za mnoge od njih zlatni rez je bio izravna veza s tim sferama, njihova manifestacija u našem nesavršenom pojavnom svijetu. Bilo bi pretjerano reći da se zlatni rez nalazi posvuda u prirodi, ali gdje god opazimo pojavu izuzetne ljepote i sklada, najčešće ćemo otkriti prisutnost zlatnog reza. On je podsjetnik na srodnost našeg pojavnog svijeta s njegovim savršenim izvorom i s njegovom potencijalnom budućom evolucijom.Autor: Suzana Dobrić |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Pet 3 Jun - 19:33 Pet 3 Jun - 19:33 | |
| Genijalni um Johna Nasha
Analizirajući karakteristike genija iz različitih područja i vremenskih razdoblja, može se uočiti mnoštvo zajedničkih osobina: izvanredne intelektualne sposobnosti, kreativnu produktivnost, snažnu intuiciju, golemu životnu energiju te upornost u traženju rješenja.
Ako ponekog genija i ne karakterizira neka od gore navedenih osobina, jedno im je ipak svima zajedničko – životni put obilježen velikim iskušenjima, profesionalnim i osobnim krizama, nerazumijevanjem okoline i tragikom. Genij je dijete tuge, rekao je jednom američki skladatelj John Adams.
John Forbes Nash, Junior (1928. – 2015.) američki je matematičar koji je postao planetarno poznat 2001. godine zahvaljujući biografskom filmu Genijalni um – blockbusteru Rona Howarda koji je za to ostvarenje dobio Oscara za režiju. Iako je film rađen na osnovi istoimene Nashove biografije koju je uz pomoć njegove supruge Alicie napisala novinarka Sylvia Nasar, ipak se u mnogočemu razlikuje od knjige, a knjiga opet od stvarnog života.
John Nash na ceremoniji dodjele Nobelove nagrade 1994. godine. Nagrade za matematiku i ekonomijuJohn Nash veliki je znanstveni um našega doba, dobitnik mnogih nagrada na području matematike i ekonomije. Jedina je osoba koja je dobila i Nobelovu i Abelovu 1 nagradu . Dodijeljena mu je Nobelova nagrada 1994. godine za ekonomiju (zajedno s Johnom Charlesom Harsanyijem i Reinhardom Seltenom), za pionirski rad na području teorije igara. Nashova zasluga u unapređenju teorije igara je teorija ravnoteže nekooperativnih igara (Nashov equilibrium ili Nashova ravnoteža) koja se smatra značajnim dostignućem u prošlom stoljeću. Nashova ravnoteža možda nije najbolje rješenje za pojedinca, ali je zato optimalno rješenje za sve sudionike. Znanstveno gledano, teorija igara povezuje matematiku s ostalim disciplinama te je doprinijela boljem razumijevanju ekonomije, sociologije, psihologije i teorije evolucije. Za doprinos teoriji nelinearnih parcijalnih diferencijalnih jednadžbi i njihovih primjena u geometrijskoj analizi dobio je Abelovu nagradu 2015. godine, zajedno s kanadsko-američkim matematičarom Louisom Nirenbergom. Jednom prilikom Nirenberg je rekao: Prije otprilike dvadeset godina netko me je pitao postoje li matematičari koje bih smatrao genijima. Mogao sam pomisliti samo na jednog te je moj odgovor bio – to je John Nash. Imao je nevjerojatan um. Razmišljao je drugačije od drugih ljudi.Bio je i na pragu osvajanja Fieldsove medalje, najprestižnije nagrade u matematici, no ipak mu je promakla i pripala je Enniu de Giorgiju jer su skoro u isto vrijeme, ali različitim metodama, obojica došla do rješenja devetnaestog Hilbertovog problema. Klice genijalnosti mladog umaNa poticaj ambiciozne majke učiteljice, naučio je čitati već s četiri godine, a u školi je preskakao razrede. U ranom djetinjstvu Johnovi učitelji nisu prepoznali njegov genijalni um, ali su detektirali nedostatak socijalnih vještina. Jednom je prilikom učiteljica obavijestila roditelje da John ne razumije matematiku, a ustvari ona nije razumjela njegov elegantniji način rješavanja matematičkih problema. U školi se izrazito dosađivao – dok bi učenici tek prepisivali zadatak s ploče, Nash bi ga promotrio i mirno iznio rješenje. No, situacija je srećom bila stimulativnija u obiteljskom okruženju. Dok su njegovi vršnjaci čitali slikovnice, otac je Johnu davao znanstvene knjige; dok su se ostali igrali loptom, John je radio znanstvene eksperimente. Znanstveni i psihološki portret u mladostiUpisuje kemiju na Carnegie institutu za tehnologiju, no završava matematiku. Na Princetonu je doktorirao 1949. disertacijom za koju će četrdeset i pet godina poslije dobiti Nobelovu nagradu. - Citat :
 Nashova ravnoteža (prema Johnu Forbesu Nashu), skup je strategija u teoriji igara s pomoću kojih se u igri postiže ravnotežno stanje bez suradnje igrača (nekooperativna ravnoteža) iako bi dobitak svima bio veći kada bi se dogovorili. Nakon što je postignuta Nashova ravnoteža, nijedan igrač ne može promijeniti svoje ponašanje a da to za njega ne znači gubitak. Ostali igrači promjenu vide kao pogrešku kojom se koriste za svoj dobitak. Nashova ravnoteža (prema Johnu Forbesu Nashu), skup je strategija u teoriji igara s pomoću kojih se u igri postiže ravnotežno stanje bez suradnje igrača (nekooperativna ravnoteža) iako bi dobitak svima bio veći kada bi se dogovorili. Nakon što je postignuta Nashova ravnoteža, nijedan igrač ne može promijeniti svoje ponašanje a da to za njega ne znači gubitak. Ostali igrači promjenu vide kao pogrešku kojom se koriste za svoj dobitak.
Primjer je uspostave Nashove ravnoteže slučaj dvojbe zatvorenika. Dvojica su osumnjičenika za pljačku banke uhićena i smještena u odvojene ćelije. Policija nema dokaze i može ih optužiti jedino na temelju njihovih priznanja. Ako obojica ne priznaju, bit će zbog prometnog prekršaja kažnjeni po godinu dana zatvora. Ako obojica priznaju, svaki će dobiti 5 godina zatvora zbog pljačke banke. Ako samo jedan od njih prizna, bit će oslobođen, dok će drugi biti osuđen na 10 godina zatvora. Svaki zatvorenik ima dvije mogućnosti: priznati ili ne priznati. Najbolje zajedničko rješenje bilo bi ne priznati. Međutim, ako nema dogovora, pojedincu je sigurnije priznati. U slučaju dvojbe zatvorenika, Nashova je ravnoteža priznanje obojice zatvorenika. Kolege su ga opisivali kao čudaka koji na klaviru stalno iznova svira istu melodiju, ostavlja sladoled da mu se topi po odjeći, hoda po svom cimeru koji spava, kako bi ugasio svjetlo. Često bi sam lutao studentskim dvorištem razmišljajući i pričajući naglas, a studenti su govorili: On je lud, ali neće nikome učiniti ništa nažao. Sugovornika bi rijetko gledao u oči, trebalo je dugo vremena da odgovori na pitanje, a ako ga je smatrao glupim, na pitanje uopće ne bi odgovorio. Kažu da je bio vrlo usamljen i izložen podsmijehu, no i sam se prema kolegama ponašao pomalo bahato, kao da mu nisu dorasli, što i nije bilo daleko od istine. Jedan je kolega rekao da je bez obzira na svu njegovu ekscentričnost, u njemu tinjala čista ljudska toplina. Sigurnost u vlastite ideje i intelektualna samouvjerenost kod njega nisu bile upitne. Kad je stigao na Princeton, posjetio je Einsteina kako bi s njim porazgovarao o nekim svojim idejama i, prema sveučilišnim tračevima, kako bi Einsteinu nešto objasnio. Poslije je sam o tom susretu rekao: Kad sam upoznao Einsteina, bio je u godinama mog djeda. Sjećam se da smo pričali o teorijama u fizici. Nije djelovao previše impresioniran onime što sam mu rekao, ali me savjetovao da bez obzira na to čime se trenutno bavim, moram ući duboko u tu materiju ako želim biti uspješan. U dvadeset i trećoj godini postaje predavač na prestižnom MIT-u (Massachusetts Institute of Technology). U skladu s karakteristikama genijalnih umova, John nije znao prenijeti znanje koje se rojilo u njegovoj glavi. Njegova su predavanja više sličila glasnim razmišljanjima i izgovaranju nepovezanih ideja, što je rezultiralo nezainteresiranošću studenata za njegove kolegije. Njegova stručnost i kompetentnost dovele su ga u vojnu organizaciju RAND, korporaciju u kojoj je radio kao konzultant na razvoju niza igara koje su služile za predviđanje strategija američkih vojnih neprijatelja. Bilo je to krajem 50-ih godina XX. stoljeća, kad se ženi kolegicom Aliciom Lopez i kad se počinju pojavljivati prvi znakovi bolesti. Godine borbe s paranoidnom šizofrenijomIako su mnogi već i ranije Johnovu čudnovatost okarakterizirali kao oblik neke psihičke bolesti, nastup je bio nagao i zastrašujući. Delirij je bio poput sna iz kojeg se nikad ne budim, rekao je jednom o tim stanjima.  Slijedilo je teško razdoblje dugotrajne terapije koje je trajalo dvadesetak godina. Činilo se da neće biti poboljšanja. Bile su to godine jasnog suočavanja sa svojim stanjem i s osjećajem bespomoćnosti da bilo što učini za svoje zdravlje. Svojevoljno i kategorično prekida sve vrste terapija te dane provodi u svom svijetu, progonjen paranojama i mučen deluzijama. Alicia se razvodi od njega, no nikada ga nije uistinu napustila. Tijekom čitavog razdoblja teške mentalne bolesti nastavio je racionalno razmišljati i rješavati probleme znanstvene probleme. Mislim da sam bio jednako uspješan u svojim istraživanjima i za vrijeme bolesti i u razdoblju prije nje, jedina razlika je u tome što bi moj rad bio bolje vrednovan i poštovan da sam bio “normalna” osoba.Sredinom osamdesetih bolest se polako povlači, a da nije bila tretirana medicinskim putem. Stručnjaci nisu imali odgovor na takav razvoj Johnovog stanja, biografi ga pripisuju Alicijinoj požrtvovnosti i ljubavi, a matematičari genijalnom umu sposobnom da u takvoj bolesti razluči zbilju od fikcije. Borio se protiv mentalne bolesti iznimnom snagom vlastite volje. 
Povratak u realnostNakon izlječenja vraća se na Princeton i službeno nastavlja s radom, premda se ustvari nikad nije ni prestao baviti istraživanjima. Tada prima i zlatno odličje za svoj rad – Nobelovu nagradu. Na primanju nagrade 1994. godine u Stockholmu u publici je sjedila Alicia, a John, tada šezdesetšestogodišnjak, držao je poduži govor. Između ostalog rekao je da je, statistički gledano, zaista nevjerojatno da bilo koji matematičar ili znanstvenik u dobi od 66 godina može kontinuirano istraživati. I zaista, u njegovim kasnijim godinama mnogi su se divili bistrini njegova razmišljanja, a i fizički je odavao dojam mnogo mlađe osobe. Mladi znanstvenici osjećali su poštovanje prema njemu, voljeli su s njim pričati, znali su da od njega mogu puno naučiti. Kad su ga u Istanbulu 2012., za vrijeme jedne matematičke konvencije pitali ima li matematika ikakve veze s poštenjem, osamdesetčetverogodišnji John je odgovorio: Naravno da ima. Cilj matematičara je da nađu istinu. To je vrlo važno. U matematici nema laganja. Izuzetno je snažna bila povezanost Johna i Alicije, jedna od onih rijetkih koje se mogu nazvati sudbinskima. Stvarnu priču njihova života teško da bi mogao tako originalno osmisliti bilo koji scenarist. Par se po drugi puta vjenčao 2001. godine, a 24. svibnja 2015., na povratku s dodjele Abelove nagrade, zajedno pogibaju u automobilskoj nesreći… Postoji veza između odstupanja od normalnog razmišljanja i pribjegavanja kreativnom razmišljanju. Ne bi mi na um pale dobre znanstvene ideje da sam razmišljao “normalno”.Postoji velika razlika između fantaziranja o idejama i uzdizanja uma do čistih ideja u nastojanju da se u obliku umjetničkog ili znanstvenog djela te ideje nesebično stave u službu i na dobrobit čovječanstva. Prvo ne zahtijeva izlazak iz svoje uobičajene zone komfora, drugo zahtijeva izuzetne psihomentalne napore i odricanja. Prvo je odlika prosječnosti, drugo genijalnosti. 1 Abelova nagrada norveška je međunarodna nagrada koju od 2003. godine dodjeljuje Norveška akademija znanosti za izuzetan doprinos na području matematike. Nazvana je prema norveškom matematičaru Nielsu Henriku Abelu te je, zajedno s istoimenom zakladom, uspostavljena na 200. obljetnicu njegova rođenja. |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Sub 11 Jun - 12:13 Sub 11 Jun - 12:13 | |
| David Hilbert  Poznati njemački matematičar David Hilbert (23.01.1862-14.02.1943) nakon završene gimnazije u rodnom gradu Königsberg upisuje se na Univerzitet u istom gradu. Doktorirao je 1885 godine, sa disertacijom "O nepromjenjivim svojstvima posebnih binarnih formi, sa naglaskom na sferne harmonijske funkcije". Godine 1884. Adolf Hurwitz, sa fakulteta u Göttingen, postaje izvanredni profesor na fakultetu u Königsbergu i ubrzo postaje Hilbertov prijatelj. Od tada njihova međusobna razmjena znanstvenih ideja ima značajan utjecaj na njihove znanstvene karijere. Hilbert je bio član nastavnog osoblja na Univerzitetu Göttingen od 1886 do 1895 godine, a godine 1895 Hilbert je postavljen za šefa katedre na Odsjeku za matematiku na Univerzitetu, u to vrijeme najboljem centru za znanstvena istraživanja u području matematike na svijetu, gdje predaje ostatak karijere. Hilbertova značajna pozicija u svijetu matematike poslije 1900 godine se ogledala u tome što su ga druge institucije dovodile u iskušenje da napusti Göttingen, a 1902. i nudile mjesto šefa katedre na Univerzitetu u Berlinu. Hilbert je odbio tu ponudu, ali nakon što je sklopio pogodbu sa Univerzitetom Göttingen, ubjedivši ih da uspostave novo mjesto šefa na koje je doveo svog najboljeg prijatelja Minkowskog.
Hilbertov prvi rad na nepromjenljivim funkcijama doveo ga je 1888. do poznatog teorema konačnosti. Dvadeset godina ranije, Paul Gordan je demonstrirao teorem o konačnosti generatora binarnih oblika koristeći vrlo komplicirane proračune koji su onemogućili poopćavanje same metode na funkcije sa više od dvije varijable. Hilbert je uočio potrebu sasvim drugačijeg pristupa. Kao rezultat demonstrirao je „Hilbertov osnovni teorem“ koji pokazuje postojanje konačnog skupa generatora neovisno o broju varijabli, u apstraktnom obliku. Objavljivanje tog rada u Mathematische Annalen mu je odbijeno s razlogom da nije sveobuhvatan i potpun te da se uopće ne radi o matematici. Međutim Hilbert je u sljedećem članku, kojeg opet šalje u Annalen, proširio svoju metodu dajući proračune o maksimalnom stupnju minimalnog seta generatora. Taj rad je ocijenjen kao najznačajnije djelo u području opće algebre koje je časopis ikada objavio.
U tekstu Osnove geometrije koju objavljuje 1899., on predlaže set tzv. Hilbertovih aksioma kojima zamjenjuje tradicionalne Euklidove aksiome. Ti aksiomi ispravljaju slabosti uočene kod Euklidovih aksioma koji su se do tada koristili doslovce kao što su napisani. Hilbertov pristup označio je prebacivanje na modernu aksiomatsku metodu. Hilbert je prezentirao, u obliku govora „Problemi Matematike“, listu neriješenih problema na internacionalnom kongresu matematičara u Parizu 1900. godine, koju je kasnije proširio na 23 problema. Tim govorom je želio zaokružiti matematički jako uspješno 19. stoljeće i predvidjeti razvoj matematike u budućnosti. Tom prilikom je rekao:
“Ako vjerujem u razvoj matematičkog znanja u bliskoj budućnosti, moramo se pozabaviti nedovršenim pitanjima i riješiti probleme koje zadaje današnja znanost, a čija rješenja očekujemo.” “Znamo da svako stoljeće nosi svoje probleme koje sljedeće stoljeće rješava ili zamjenjuje novim.” “Kraj sjajne epohe poziva nas da se osvrnemo na prošlost, ali i da pogledamo u nepoznatu budućnost.”
Hilbertovi problemi uključuju hipotezu kontinuuma, konzistentnost aksioma aritmetike, Rimanovu hipotezu i druge. Za vrijeme prošlog stoljeća mnogi su problemi i riješeni, i svako riješenje je bio značajan događaj za matematiku.
Danas se Hilberovo ime pamti kroz koncept Hilbertovog prostora. Matematički koncept Hilbertovog prostora generalizira pojam Euklidovog prostora na način da proširuje metode vektorske algebre sa 2-dimenzionalnog i 3-dimenzionalnog prostora na beskonačno dimenzionalan prostor. To je apstraktni vektorski prostor u kojemu udaljenosti i kutovi mogu biti izmjereni i cijeli se nalaze u tom prostoru. Još jedan od razloga uspjeh teorije Hilbertovog prostora je i u činjenici da iako se mogu razlikovati po porijeklu i izgledu, većina Hilbertovih prostora gledano u matematici i fizici, su samoumnožena manifestacija jednog odvojenog Hilbertovog prostora.
Hilbert je dao doprinos u mnogim granama matematike: teorija brojeva, funkcionalna analiza, integralne jednačine itd. Iako je bio isključivo matematičar, Hilbert je u jednom periodu bio posvećen i fizici, istraživao je i teoriju relativnosti.
Među Hilbertovim učenicima bili su: Hermann Weyl, šahovski prvak Emanuel Lasker, Ernst Zermelo, Carl Gustav Hempel i kasnije poznati matematičari: Otto Blumenthal (1898.), Felix Bernstein (1901.), Hermann Weyl (1908.), Richard Courant (1910.), Erich Hecke (1910.), Hugo Steinhaus (1911.), Wilhelm Ackermann (1925.). Na fakultetu je bio okružen s nekima od najznačajnijih matematičara 20. stoljeća, kao što su Emmy Noether i Alonzo Church.
Hilbert je primio i počast od Akademije znanosti u Mađarskoj 1905 godine, a 1930. je proglašen počasnim građaninom Königsberg.
Hilbertov entuzijazam za matematiku i posvećenost riješavanju matematičkih problema tokom cijelog njegovog života je iskazana kroz njegovih šest poznatih riječi - Mi moramo |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Sub 18 Jun - 8:47 Sub 18 Jun - 8:47 | |
| |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Sub 18 Jun - 8:50 Sub 18 Jun - 8:50 | |
| |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Uto 28 Jun - 18:09 Uto 28 Jun - 18:09 | |
| |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Uto 28 Jun - 18:10 Uto 28 Jun - 18:10 | |
| |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Uto 28 Jun - 18:11 Uto 28 Jun - 18:11 | |
| |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Uto 28 Jun - 18:11 Uto 28 Jun - 18:11 | |
| |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Sub 6 Avg - 9:10 Sub 6 Avg - 9:10 | |
|  6*10:2*4-5!=60:2*4-5!=30*4-5!=120-120=0 6*10:2*4-5!=60:2*4-5!=30*4-5!=120-120=0 |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Sub 6 Avg - 9:12 Sub 6 Avg - 9:12 | |
| |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Sub 6 Avg - 9:22 Sub 6 Avg - 9:22 | |
| Prvu matematičku mašinu konstruisao je Blez Paskal, poznati francuski matematičar, fizičar i filozof, sa samo 18 godina. Cilj prvog mehaničkog kalkulatora bio je da pomogne njegovom ocu u poslovanju.
Leonard Ojler, bio je švajcarski matematičar i smatra se jednim od najuticajnijih matematičara 18-og veka. Uveo je pojam funkcije i prvi je upotrebio oznaku f(x) za funkciju f primenjenu na argument x. Pored toga, uveo je moderan zapis trigonometrijskih funkcija, slovo e kao oznaku za osnovu prirodnog logaritma (danas poznatu i kao Ojlerov broj), grčko slovo Σ za označavanje sumiranja i slovo i za označavanje imaginarne jedinice. Takođe je koristio grčko slovo π da označi odnos obima i prečnika kruga, iako to nije bila originalno njegova ideja. Zaslužan je i za velika otkrića u korišćenju grafika.
Karl Fridrih Gaus, bio je jedan od matematičkih velikana koji je doprineo razvitku matematike svojim radom u oblati geometrije, statistike, teorije brojeva, algebre itd.
Emi Neter, bila je jedna od retkih žena matematičara koju je sam Albert Ajnštajn opisao kao najkreativniju i najvažniju ženu u istoriji matematike. Iako je potpuno nezasluženo ostala slabo poznata javnosti, svojim radom dala je velik doprinos algebri i fizici.
Bernhard Riman, bio je nemački matematičar koji je dao veliki doprinos u razvoju matematičke analize i diferencijalne geometrije. Svojim radom praktično je omogućio kasniji razvoj Ajnštajnove opšte teorije relativiteta.
Jedna od poznatijih britanskih matematičara bio je Alan Tjuring. Pored matematike bio je poznat i kao priznati logičar i kriptograf. Tokom drugog svetskog rata radio je na razbijanju nemačkih šifri.
Zbog svojih dostignuća u kreiranju koncepta algoritama, kao i računanja pomoću Tjuringove mašine, smatra se ocem modernog računarstva. Tjuringov test dao je ogroman značaj prilikom definisanja veštačke inteligencije, tj. da li će ikada biti moguće reći da mašina može da misli.
Radio je na softveru jednog od prvih računara, a takođe je napisao i šahovski program koji je sam simulirao 1952. godine, koji je jednom pobedio i izgubio partiju. |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Sub 6 Avg - 9:25 Sub 6 Avg - 9:25 | |
| Džon Horton Konvej, bio je engleski matematičar rođen 1937. godine a velik doprinos matematici dao je kroz oblasti grupne teorije, teorije brojeva i geometrije, ali je ipak najpoznatiji po pravilima igre Game of Life, koju je i ustanovio.
Terens Tao, rođen je 1975. godine. dobitnik je Fildsove medalje. Poznat je po otkriću do kojeg je došao sa svojim saradnikom Benom Grinom. Oni su otkrili da je moguće pronaći nizove prostih brojeva bilo koje dužine u kojima se svaki broj jednako udaljen od narednog broja. Na primer 11, 17, 23, 29 predstavljaju 4 prosta broja gde je svaki broj udaljen od narednog za 6 mesta.
Ruski matematičar Grigori Perelman, rođen je 1966. godine i smatra se najvećim matematičkim umom današnjice. Uspeo je da reši jedan od najtežih matematičkih zadataka svih vremena, Poenkarovu hipotezu. Mnogi naučnici pokušavali su da je reše i radili na tome više od 100 godina, međutim Perelman je prvi kome je to pošlo za rukom.
Upravo zbog toga određen je za dobitnika Fildsove medalje 2006. godine, međutim on je odbio nagradu koja se inače smatra Nobelovom nagradom u matematici.
Kasnije je odbio i nagradu od milion dolara koju dodeljuje institut Klaj (Clay Millennium) za rešenje svakog od 7 milenijumskih problema u matematici. Iako živi sa majkom i sestrom u velikom siromaštvu on je svoju odluku potkrepio rečima:
“Ja znam kako da upravljam svemirom. Recite mi, zašto bi trebalo da jurim milion dolara? Nisu mi potrebni“.
Pal Erdeš bio je mađarski matematičar rođen 1913. godine. Ono što je bilo karakteristično za njega je da nije voleo da živi na jednom mestu, već je živeo od univerziteta do univerziteta tj. od kampusa do kampusa.
Njegova odlika je bila i ta da nije voleo da objavljuje svoje radove sam, već je sarađivao sa 500 saradnika i sa njima objavio oko 1500 radova. Njegova dostignuća bila su iz oblasti kombinatorike, teorije grafika i brojeva, klasične analize, teorije aproksimacije, teorije skupova i verovatnoće. |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Sub 6 Avg - 9:40 Sub 6 Avg - 9:40 | |
| Reč matematika potiče od grčke reči máthēma, koja znači učenje, studije, nauka.
Broj 5 se na tai jeziku izgovara kao “ha”. Zato se 555 često koristi kao skraćenica u slengu za “hahaha”.
Znate li za izraz diskalkulija? Diskalkulija znači da neko teže uči računanje, što može da bude izraženo kao nemogućnost da razume brojeve ili da nauči činjenice iz matematike.
Zaseci i udubljenja na skeletima životinja dokazuju da su ljudi računali i bavili se matematikom mnogo pre nego što je ona nastala kao nauka, još 30.000 dodina p.n.e.
Nula (0) je jedini broj koji ne može da se predstavi rimskim brojevima.
Engleska reč za nulu, zero, nastala je od arapske reči sifr, koja je takođe dala i reč šifra, što znači ”tajni način pisanja”.
Znate li za magiju broja 9? Pomnožite bilo koji broj sa 9 i zatim saberite sve pojedinačne cifre rezultata (proizvoda) dok ne dobijete jednu cifru. Zbir ovih cifara daće vam 9.
Evo interesantnog načina da proverite deljivost sa brojem 3. Broj je deljiv sa 3 ako je zbir njegovih cifara deljiv sa 3.
Znak jednakosti (=) je izumeo matematičar iz XVI veka, Robert Record, jer mu je dosadilo da piše “je jednako” u jednačinama.
Broj Googol (po kome je pretraživač Google dobio ime, samo sa greškom u spelovanju) koristi se da se izrazi broj 1 praćen sa 100 nula i prvi ga je upotrebio 9-ogodišnjak Milton Sirotta još 1940. godine.
Abakus se smatra direktnim pretkom digitrona.
12.345.678.987.654.321je proizvod brojeva 111.111.111 x 111.111.111. Primećujete da se cifre u broju penju od 1 do 9 i nazad.
Znaci za plus (+) i minus (-) koriste se još od 1489. godine.
Ikosaedar je geometrijski oblik sa 20 strana. Koliko god vam to neobično zvučalo, to je jedan od 5 pravilnih poliedara.
Ako sabirate brojeve od 1 do 100 redom, zbir je 5.050. Parovi 1 i 100, 2 i 99, 3 i 98 i tako redom, uvek daju zbor 101. Takvih parova je 50 (100 / 2), dakle, 101 x 50 = 5.050.
2 i 5 su jedini prosti projevi koji se završavaju sa 2 ili 5.
Trenutak ili momenat je zapravo prava jedinica za vreme koja označava 1/100 deo sekunde.
U grupi od 23-oje ljudi, bar dvoje imaju isti dan rođenja sa verovatnoćom većom od 50%.
Ako ima 50 učenika u razredu, gotovo da je sigurno da će dvoje biti rođeni istog dana.
Od svih geometrijskih oblika koji imaju isti obim, krug ima najveću površinu.
Od svih geometrijskih oblika koji imaju istu površninu, krug ima najmanji obim.
U gradu Tajpej, na Tajvanu, građanima je 1995. godine dozvoljeno da uklone cifru 4 iz uličnog broja zato što se izgovara isto kao i reč smrt na kineskom. Zbog toga mnoge bolnice u Kini nemaju 4. sprat.
Grčki matematičar Pitagora je u izračunavanju jednačina koristio malo kamenje. Otuda je ime kalkulator nastalo od grčke reči za šljunak.
U mnogim kulturama broj 13 smatra se baksuznim i postoji mnogo mitova o tome. Na primer, u mnogim starim evropskim religijama bilo je 12 dobrig bogova, a loš bog je nazivan 13. bog. Drugo sujeverje potiče od Poslednje večere – bilo je 13 ljudi za trpezom, uključujući i Isusa, a Juda se smatra 13. gostom.
Da li ste čuli za Fibonačija i njegov niz? To je niz brojeva u kojem je svaki broj zbir prethodna dva broja. Evo, na prmer: 1, 1, 2, 3, 5, 8, 13, 21, 34, i tako dalje. Semenke na suncokretu poređanu su upravo po ovom nizu!
Da li ste čuli za broj palindrom? To je broj koji se isto čita sa obe strane, na primer: 12421.
Arapski brojevi kao što su 1, 2, 3… nastali su pre više od 1.000 godina.
Broj π (pi) ne može da se izrazi kao razlomak, što ga čini iracionalnim brojem. Takođe je i beskonačan. Ovako broj Pi izgleda kada je napisan sa 100 decimala:
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679 |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Ned 7 Avg - 8:44 Ned 7 Avg - 8:44 | |
| |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Ned 7 Avg - 8:49 Ned 7 Avg - 8:49 | |
| Obrazac koji pokazuje kako da zapamtiš vrijednost broja e sa tačnošću od 15 decimalnih mjesta nije komplikovan. Zapamti zanimljiv obrazac gdje se poslije 2,7 pojavljuje 1828 dva puta:
2,7 1828 1828
Sljedeći niz sadrži uglove jednakokrakog pravouglog trougla – 45°, 90°, 45°:2,7 1828 1828 45 90 45 |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Ned 7 Avg - 9:31 Ned 7 Avg - 9:31 | |
| Množenje brojem 11 najlakšeje u množenju dvocifrenih brojeva
63*11=693
6 (6+3) 3
693
52*11=572
5(5+2)2
572 |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Uto 27 Sep - 9:30 Uto 27 Sep - 9:30 | |
| Engleski fizičar i plemić Lord Kevin, koji je živio i djelovao u 19. st., pukim nagađanjem je pretpostavio da su kemijski elementi zapravo čvorovi u eteru. U tom slučaju vodik bi bio jedna vrsta čvora, kisik druga, dušik treća i tako dalje kroz čitav periodni sustav elemenata; svaki element zasebno bi predstavljao određenu vrstu čvora sa uvojima i zakretajima samo njemu svojstvenim. Prema takvom konceptu Peter Guthrie Tait je sastavio detaljima popraćenu i vizualno impresivnu tablicu čvorova u nastojanju da prikaže (makar većina čvorova izgleda upravo identično) sve njihove međusobne razlike. No s gledišta fizičara, Kelvin i Tait su bili na krivom tragu; prema gledištu tada novootkrivene grane nuklearne fizike, atomske fizike, koja pojašnjava građu atoma od kojih se sastoje elementi, teorija čvorova je neosnovana i zastarjela. Tako eksplikacije koje ona zastupa bivaju uvrštene u antologiju znanstvenih teorija kao još samo jedan od nadahnutih i složenih pokušaja tumačenja prirodnih elemenata, no nažalost ipak pogrešnih.No s druge strane, prema viđenjima matematičara, koncepcija čvorova i njihovo tumačenje je itekako dokazalo svoju svrhovitost utrvši putove novoj grani matematike, koja prva znanstveno preuzima i službeno nosi naziv teorija čvorova.U svom članku naziva ''Kombinacijska revolucija u teoriji čvora'', koji je objavljen u prosincu 2011. fizičar i matematičar Sam Nelson opisuje novi pristup teoriji čvora, koji je posljednjih godina osobito dobio na aktualnosti. Također, važno je napomenuti da je pri pravilnoj evaluaciji objekata koji su definirani kao predmet istraživanja teorije potrebno imati na umu širok spektar raznolikih predmeta i supstanci koje mogu biti u različitim agregatnim stanjima, a pritom imati oblik tj. obilježje čvora. Potencijalni čvorovi različitih namjena mogu postojati u najrazličitijim oblicima pojavnosti. Kako mornari u području svoje djelatnosti zasigurno najviše upotrebljavaju konope odnosno čvorove, upravo njima je zasigurno već dugo poznato da postoje različite vrste čvorova, štoviše; broj mogućih varijanti namotaja i ispreplitanja je gotovo neograničen.Pojam matematički čvor predstavljen je zamišlju zamršenog kruga: zamislite perec-zamršeni krug tijesta, ili primjerice lastiš, koji je zapravo razmršen jer nema oblik čvora. Matematičari proučavaju uzorke, razmjere, simetrije i nepravilnosti čvorova kako bi proizveli i usavršili tehnike pomoću kojih nastoje uočiti i najminucioznije moguće razlike dvaju čvorova. Matematički, moguće je zamisliti uzicu, odnosno crtu koja konstituira čvor kao jednodimenzionalni objekt, a čvor sam po sebi bi trebao egzistirati u trodimenzionalnom prostoru. Projekcije, nalik onima kakve je crtao Tait, su zapravo modeli trodimenzionalnog čvora na dvodimenzionalnoj podlozi. Prilikom crtanja takvih skica, uobičajeno je povući pune i prekinute linije kako bi se prikazali prijelazi ispod i iznad pri točkama namotaja. Ukoliko se tri ili više niti čvora ukrštavaju u istoj točci grananja, moguće ih je malo pomaknuti bez da se čvor promijeni, tako da je svaka točka u ravnini postavljena ispod najviše dvije niti čvora.Planski dijagram čvora je shema trodimenzionalnog čvora nacrtanog u dvodimenzionalnoj ravnini , u kojoj svaka točka dijagrama može predstavljati najviše dvije točke čvora. Takvi dijagramski prikazi se već dugo primjenjuju u matematici kao polazište za studije čvorova.Kako Nelson izvještava u svom članku, matematičari su osmislili različite načine prikaza informacija koje su sadržane u dijagramu čvorova. Jedan od modela je Gaussov kod, koji se sastoji od niza slova i brojki, a svako ukrštavanje u čvoru je označeno simbolom O ili U, ovisno o tome ide li uzica odnosno ukrštavajući namotaj ispod ili iznad uzičnog nastavka. Tako Gaussov kod za jedan jednostavan čvor izgleda primjerice ovako: O1U2O3U1O2U3.Sredinom devedesetih znanstvenici su otkrili jednu veoma neobičnu činjenicu koja mora pronaći svoje mjesto u dotada standardiziranoj teoriji. Naime ustanovljeno je da postoje određeni Gaussovi kodovi kod kojih je nemoguće grafički prikazati planski model, tj. dijagram čvora, no u većini uvjeta se sheme prikazane kodom ipak ponašaju kao čvorovi. U konkretnom slučaju, ti kodovi koje Nellson naziva neplanski Gaussovi kodovi savršeno funkcioniraju u formulama koje služe kao indikatori u dokazivanju karakteristika koje čine osnovu čvora kao takvog. Nelson objašnjava: Planski Gaussov kod uvijek opisuje čvor u tri dimenzije: no kakvu vrstu informacije može opisivati neplanski kod? Prema rezultatima takvog istraživanja čvorovi koji su legitimno prikazani Gaussovim kodom, a čija svojstva se ne podudaraju s mogućnošću realizacije u trodimenzionalnom prostoru zaista postoje. Takve virtualne čvorove je moguće istraživati jedino putem pomnog planiranja korištenja stručnih kombinatornih tehnika za procjenu i analizu dijagrama čvora.Inženjerski pomno integriranom i kompleksnom studijom čvorova i pripadajućih jednadžbi u matematici, znanstvenici su ustanovili da ipak postoje neki općeniti oblici čvorova kakve češće pronalazimo u prirodi, te koji su sukladno tome ne samo tipičniji već i funkcionalniji u grananju svojih niti, neovisno o tome prenose li one elektroničke impulse ili učvršćuju određeni objekt.Neovisno o dotadašnjim postavkama, neupitno je da ćemo u budućnosti svjedočiti novim otkrićima ove ne tako davno propupale grane matematike. Izvor: American Mathematical Society |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Čet 29 Sep - 9:34 Čet 29 Sep - 9:34 | |
| Što je tako posebno kod broja 666? To je zbroj svih brojeva na kotaču ruleta, to je broj dvostrukog trokuta, a također je jednako zbroju kvadrata prvih sedam prostih brojeva. Ali to nije ono na što većina ljudi pomisli kada čuje 666.
Za većinu ljudi broj 666 ima jedno specifično značenje: ushićenje, apokalipsa, kraj svijeta – zovite ga kako hoćete, predznak mu je broj 666. Sve je zapisano upravo tamo u Knjizi Otkrivenja: "Neka ima razum računati broj zvijeri, jer to je broj čovjeka; a broj mu je šest stotina šezdeset i šest."
Zvuči sablasno, no o čemu je zapravo riječ? Zašto bi zvijer uopće imala broj, a kamoli prilično običan poput 666? Pa, evo u čemu je stvar: Knjiga Otkrivenja je prilično bizarna, a i ozbiljni znanstvenici religije kažu isto.
"Knjiga Otkrivenja je vrlo različita od bilo čega drugog što nalazite u Novom zavjetu", objasnila je profesorica religije Harrington Spear Paine s Princetona, Elaine Pagels. "Nema moralnih propovijedi ili etičkih ideja ili drugih poučnih stvari. Sve su to vizije. Zato je toliko privlačna umjetnicima, glazbenicima i pjesnicima tijekom cijelog stoljeća."
I postoji dobar razlog za to: "to je ratna literatura", rekla je Pagels, koju je napisao "Ivan" - vjerojatno izbjeglica iz Jeruzalema, koji su Rimljani uništili u Prvom židovsko-rimskom ratu. "To proizlazi iz tog rata i dolazi od ljudi koji su uništeni ratom", dodala je.
Kada se pogleda na taj način, tekst počinje izgledati puno manje kao vizija doslovne apokalipse, a nešto više kao nešto što biste očekivali pronaći na satu terapijskog pisanja. Spominje se velika grimizna zvijer koja, na primjer, ima sedam glava i sedam kruna - što nije nešto što ćete vjerojatno vidjeti u stvarnom svijetu, već tanko prikrivena referenca na dinastiju Julija Cezara, objasnila je Pagels.
"Većina ljudi misli da je Ivan pisao oko 90. godine u prvom stoljeću. To bi bilo 60 godina nakon Isusove smrti, a erupcija Vezuva dogodila se 79. godine", rekla je. "Mnogo od onoga što nalazimo u Knjizi Otkrivenja sadržano u fantastičnim slikama su opisi događaja koji su za Ivana bili vrlo bliski — rat u Jeruzalemu, erupcija Vezuva, rimski carevi koji su vladali u to vrijeme."
I upravo je taj posljednji primjer ključan za razumijevanje važnosti broja 666 - pa, to i malo numerologije. Sjetite se da je to bilo mnogo prije pojave hindusko-arapskih brojeva, a suvremeni bi čitatelji navikli na niz abecednih prikaza brojeva. "Ovo sada znači da svaka riječ ima i numeričku vrijednost", objasnio je Pete Watts iz Numberphilea u videu kanala "666". Tko bi onda mogla biti ta tajanstvena "Zvijer"?
Pa, pogledajmo dokaze: autora Otkrivenja Rimljani su natjerali da napusti svoj dom, doživio je i val državno odobrenog nasilja i neprijateljstva protiv kršćana, također od strane Rimljana. Za obje ove katastrofe bio je nadležan car Neron, koji je, unatoč tome što je bio mrtav do trenutka kada je Otkrivenje napisano, mnogi ljudi bili uvjereni da će se u bilo kojem trenutku vratiti. Može li se "Zvijer" odnositi na Nerona?
"Caesar Nero" preveden na hebrejski je נרון קיסר – ili, da se piše slovo po slovo, nun-resh-vav-nun qof-samek-resh. Svako od ovih slova ima vrijednost u hebrejskim brojevima, a ako zbrojimo vrijednosti slova u "Cezaru Neronu", onda ćemo dobiti - 666.
"Ivan bi želio da njegovi čitatelji to razumiju", objasnila je Pagels. "Taj broj, koji je utaban u tajanstvenu šifru, bi njegovi čitatelji shvatili kao ime jednog od onih careva koji su uništili njegov narod."
Dakle, ne prava zvijer, ne antikrist, samo osobito antikršćanski car koji je stvarno zeznuo pisca Otkrivenja - i koji bi se očito mogao vratiti svakog trenutka. "Nitko ne želi napisati knjigu pod carskim progonima u kojoj kaže: 'Korijen svih zala je Neron Cezar'", dodao je Watts u videu Numberphile. "Nećeš to sricati." |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Sub 1 Okt - 7:17 Sub 1 Okt - 7:17 | |
| Arhimed (287. g. pr. Kr. – 212. g. pr. Kr.) je najznamenitiji matematičar i fizičar antičkog doba. Najveći dio svog života je proveo u rodnoj Sirakuzi, ali je neko vrijeme živio u Aleksandriji. Postavio je osnove statike čvrstih tijela i hidrostatike te je nizom djela pridonio razvoju znanosti. Pročitajte kratak tekst o njegovoj smrti tijekom II. rata između Rimljana i Kartažana.
Pretor M. Klaudije Marcel je 213. g. pr. Kr. opsjeo Sirakuzu. Grad je bio snažno utvrđen i opremljen obrambenim spravama čija se izrada pripisuje Arhimedu. Usprkos izričitoj Marcelovoj zapovijedi da se Arhimedu poštedi život neki ga je rimski vojnik pri zauzimanju Sirakuze ubio. Priča se da je Arhimed u vrtu svoje kuće crtao geometrijske likove u pijesku, razmišljajući o jednom matematičkom problemu. Vojniku koji je stupio na pijesak navodno je doviknuo
Ne dirajte moje kružnice! (Noli turbare circulos meos!).
To su bile posljednje Arhimedove riječi. |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Ned 16 Okt - 6:56 Ned 16 Okt - 6:56 | |
| Mala tačka na komadu kore koji predstavlja prastari indijski matematički dokument (Bakhshali rukopis) označava jedan od najvećih događaja u historiji matematike. Tačka predstavlja prvu do sada zabilježenu upotrebu nule. Čak šta više, istraživači sa oksfordskog univerziteta, koji su u skorije vrijeme i otkrili ovaj dokument procijenili su njegovu starost 500 godina više nego što se do sada smatralo, tj. da datira iz trećeg ili četvrtog vijeka.
Danas bi bilo nemoguće zamisliti matematiku bez nule. U pozicionom brojnom sistemu, kakav je decimalni brojni sistem koji svakodnevno koristimo, mjesto cifre je jako važno, jer je ogromna razlika između brojeva 100 i 1 000000.
Međutim u ljudskoj historiji hiljadama godina smo bili bez nule. Sumerani, 5000 prije nove ere, su koristili pozicioni sistem, ali bez nule. U nekoj osnovnoj formi, koristio se simbol da bi se razlikovalo npr 204 i 20000004. Ali simbol se nikada nije koristio na kraju broja, tako da se razlika između 5 i 500 određivala na osnovu konteksta.
Kasniji dolazak nule bio je dijelom i odraz negativnih stavova koje su neke kulture povezivale uz pojam ništa. Grčki mislilac Parmenides iz 5-tog stoljeća prije nove ere je izjavio da ništa ne može postojati, jer treba govoriti o nečemu što postoji. Ovaj Parmenidski pristup se dugo zadržao kroz historiju.
Nakon pojave krščanstva, vjerske vođe u Evropi su tvrdile da pošto je Bog u svemu što postoji, ono što predstavlja ništa mora biti da je sotonističko. U pokušaju da spase čovječanstvo od đavola, odmah su izbacili nulu iz postojanja, iako su je trgovci nastavili potajno koristiti.
Nasuprot tome, u budizmu je pojam ništavilo središnja ideja na putu ka nirvani. Engleska riječ “zero” originalno je izvedena iz hindu riječi “sunyata”, što označava ništa i centralni je koncept u budizmu.
Jednostavna metoda računanja uz pomoć nule je omogućila matematičarima da se bave složenijim problemima i proučavaju opća svojstva brojeva, kao što se vidi u radovima indijskog matematičara i astronoma Brahmagupte iz sedmog stoljeća.
Perzijski matematičar Al-Hwarizmi iz devetog stoljeća bio je prvi koji je pažljivo bilježio i iskoristio ove aritmetičke upute, što je na kraju učinilo abaskus zastrajelim. Takvi mehanički setovi instrukcija pokazali su da se dijelovi matematike mogu automatizirati. A to će na kraju i dovesti do razvoja savremenih računara. Zapravo riječ “algoritam” za opisivanje skupa jednostavnih instrukcija proizilazi iz njegovog imena Al-Hwarizmi.
Godine 1200 italijanski matematičar Fibonači, koji je donio decimalni sistem u Evropu, napisao je: “Metoda indijaca nadilazi sve poznate metode za računanje. To je čudesna metoda. Računaju koristeći devet figura i simbol nula.” Dakle nakon što je nula nastala u drevnoj Indiji, trebalo je gotovo 1000 godina da se prihvati u Evropi, mnogo duže nego u Kini i na Bliskom istoku.
Izum nule takođe je stvorio novi, tačniji način opisivanja frakcija. Dodavanje nula na kraju broja povečava njegovu veličinu, a uz pomoć decimalne tačke, dodavanje nula na početku smanjuje njegovu veličinu. Postavljanje beskonačno mnogo cifara desno od decimalne tačke odgovara beskonačnoj preciznosti. Ta preciznost je upravo ono što su mislioci iz 17 vijeka Isak Njutn i Lajbnic trebali da bi razvili infinitezimalni račun. I tako su algebra, algoritam i infinitezimalni račun, kao temelji savremene matematike, ustvari nastali kao rezultat oznake za ništa. Izum nule je neizmjerno pojednostavio računanje, oslobađajući matematičare da razviju vitalne matematičke discipline kao što su algebra i račun, a time i baznu osnovu za pojavu računara.
|
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Ned 16 Okt - 7:02 Ned 16 Okt - 7:02 | |
| Mjesec (lat. Luna) je Zemljin prirodni satelit i ujedno najbliže nebesko tijelo. Mjesec, sa Zemlje, je prostim okom vidljiv samo kad je obasjan sunčevom svjetlošću. Otuda i mjesečina koju vidimo da „dolazi“ sa Mjeseca ne generiše Mjesec nego Sunce i to je zapravo sunčeva svjetlost koja se odbija od površine Mjeseca. Obasjanost Mjeseca ovisi o međusobnom položaju Sunca, Zemlje i Mjeseca, i ona određuje mjesečeve faze (mijene).
U sunčevom sistemu pola sferičnog objekta koji je okrenut prema Suncu svijetli, a druga polovina koja je okrenuta od Sunca je u tami. Dakle polovina Zemlje je uvijek osvjetljena, i polovina Mjeseca je uvijek osvjetljena. Drugo, Mjesec se okrene oko Zemlje u toku jednog mjeseca. To je period za koji prođe ciklus mjesečevih faza, što ukazuje da su faze Mjeseca povezane sa položajem Mjeseca u njegovoj orbiti oko Zemlje. Da biste vidjeli kako ova geometrijska slagalica radi, zamislite da gledate Zemlju i Mjesec daleko iznad njihovih sjevernih polova. Zamislite takođe da svjetlost od Sunca dolazi sa desne strane, tako da su desne polovine Zemlje i Mjeseca osvjetljene, a da su lijeve polovine u tami. Kako se pojavljivanje osvjetljene polovine Mjeseca mijenja iz naše tačke gledišta na Zemlji? Kada je Mjesec u dijelu svoje orbite između Zemlje i Sunca, mi na Zemlji gledamo direktno na neosvjetljenu polovinu Mjeseca. Ovo je geometrijski odnos koji dovodi do pojave novog Mjeseca ili mlađaka. Dve nedelje kasnije, kada je Mjesec na suprotnoj strani Zemlje od Sunca, mi na Zemlji vidimo potpuno osvetljenu polovinu Mjeseca. Ovo je geometrijski odnos koji dovodi do punog Mjeseca. Tokom druge dvije četvrtine ciklusa Mjeseca, linija svijetli/tamni Mjesec pada direktno usred Mjeseca sa naše tačke gledišta. Tako vidimo da je Mjesec pola osvetljen. Tokom jednog mjesečevog ciklusa posmatrano kroz 4 primarne faze svjedoci smo geometrije na nebu. Naime mjesečeve faze su podjeljenje u 4 primarne plus 4 srednje. Primarne faze su glavne pozicije poravnjanja geometrije sistema Zemlja-Mjesec i Sunca. Prva faza, pojava mladog Mjeseca ima vrijednost ugla 0 ° (360 °) između sistema Zemlja-Mjesec i Sunca. Mladi mjesec ili mlađak se desi kada su Mjesec i Sunce u savršenom poravnanju (od geometrijskog centra do geometrijskog centra). Drugim riječima, kada se Mjesec nalazi između Zemlje i Sunca, njegova osvetljena strana okrenuta je Suncu i on se sa Zemlje ne vidi ili vidi se samo jedan njegov mali deo u vidu tankog srpa. Nakon pojave mladog Mjeseca, Mjesec nastavlja svoj put oko Zemlje u smjeru suprotnom smjeru kazaljke na satu. S obzirom da se ugao između Sunca i sistema Zemlja-Mjesec sada povećava, uočavamo svjetlost sa osvjetljene strane Mjeseca. U ovoj prvoj primarnoj fazi Mjesec se kreće kroz nebo oko 14 stepeni svakog dana, što znači da će Mjesec nakon 7 dana i 9 sati putovati po nebu i kad bude ugao 90 ° između sistema Zemlja-Mjesec i Sunca, tada nastupa drugu fazu (prva četvrt) i pojavljuje se polumjesec koji postaje sve veći i veći do pojave punog Mjeseca, jer se ugao između Sunca i sistema Zemlja-Mjesec na nebu povećava usljed pomjeranja Mjeseca daleko od Sunca u orbiti oko Zemlje.
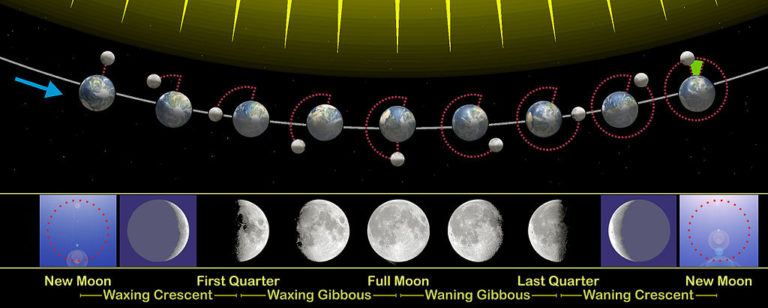
Pun Mjesec je, još jedan trenutak poravnjanja. To je trenutak opozicije, kada je Mjesec upravo na suprotnoj strani Zemlje od Sunca. U trećoj fazi kad je pun Mjesec tada je ugao od 180 °, jer je sistem Zemlja-Mjesec u suprotnom pravcu od Sunca, tj. Mjesec je između Zemlje i Sunca. Zatim se osvijetljena strana Mjeseca postupno smanjuje i ponovno prividno približava Suncu, i sve je manje njegove površine obasjano svjetlošću, te se nakon 29,5 dana vraća u položaj gdje započinje ponovo novi ciklus kao mladi Mjesec ili mlađak. To je četvrta faza (posljednja četvrt) kada je ugao od 270 ° kako se sistem Zemlja-Mjesec dalje kreće oko Sunca sve do vraćanja na početak mjesečevog ciklusa kad je ugao 0 ° (360 °) i ponovne pojave mladog Mjeseca. Prilikom mjesečevih faza dešavaju se i najsjajniji fenomeni, a to su pomračenje Sunca ili Mjeseca. Za vrijeme faze mladog Mjeseca, Mjesec može da zakloni Sunce i tada nastaje pomračenje Sunca. A za vreme faze punog Mjeseca, Mjesec može da uđe u Zemljinu sjenku i tada dolazi do pomračenja Mjeseca, koje može biti potpuno, djelimično i u polusjenci. Ovaj lunarni ciklus sa mjesečevim fazama će se nastaviti sve dok Sunce sija. Dok god Zemlja kruži oko Sunca, i sve dok Mjesec kruži oko Zemlje, oni će nastaviti ovaj večni ples kroz mjesečeve faze koje čine lunarni ciklus. Važno je spomenuti da sve ove dinamike svjetlosti i sjenke i perspektive ne mogu postojati bez sferičnog Mjeseca, Zemlje i Sunca. |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Ned 16 Okt - 7:02 Ned 16 Okt - 7:02 | |
| Istraživači sa UBC (University of British Columbia Okanagan) univerziteta pronašli su matematički model kako putovati kroz vrijeme. Ben Tippett, instruktor matematike i fizike na UBC univerzitetu, nedavno je objavio studiju o izvodivosti putovanja kroz vrijeme. Tippett, ekspert za Ajnštajnovu teoriju relativnosti, van svojih predavanja, proučava crne rupe i znanstvenu fiziku. Pomoću matematike i fizike napravio je formulu koja opisuje metod za putovanje kroz vrijeme. „Ljudi misle o putovanju kroz vrijeme kao o nekoj fikciji", kaže Tippett. „I mi mislimo da to nije moguće, jer zapravo to ne činimo, no matematički je moguće." 
Otkako je Herbert George Wells 1885. godine objavio knjigu Vremenska mašina, pojavila se znatiželja za putovanje kroz vrijeme, a naučnici su radili na rješavanju ili opovrgavanju te teorije. Godine 1915 Albert Ajnštajn je objavio teoriju opće relativnosti, navodeći da je gravitacija zakrivljenost prostora-vremena (prostor-vrijeme je fizikalni pojam koji se najčešće povezuje sa Ajnštajnovom teorijom relativnosti, a objedinjuje prostorne dimenzije i vremensku dimenziju u jednu pojavu). Više od 100 godina kasnije, LIGO Sceintific Collaboration (projekat međunarodnog tima istraživača sa mnogih instituta i univerziteta) objavio je da su otkriveni gravitacijski talasi nastali sudaranjem crnih rupa udaljenih milijardama svjetlosnih godina, i time potvrdio Ajnštajnovu teoriju.Podjela prostora u tri dimenzije, s vremenom kao posebnom dimenzijom sama po sebi, nije tačna, kaže Tippett. Sve četiri dimenzije trebaju biti istovremeno zamišljene, gdje su povezani različiti smjerovi, kao jedan četverodimenzionalni (prostor-vrijeme) kontinuum. U „ravnom" (nezakrivljenom) svemirskom prostoru, planete i zvijezde bi se kretale po ravnim linijama. Međutim masivna tijela zakrivljuju okolni prostor, a to zakrivljenje određuje kako će se druga tijela u tom prostoru kretati. Stoga u blizini masivne zvijezde, geometrija prostor-vrijeme postaje zakrivljena i ravne putanje obližnjih planeta će slijediti krive i savijati se oko zvijezde. „Vremenski pravac prostor-vrijeme takođe pokazuje zakrivljenost. Postoje dokazi da što se je bliže crnoj rupi vrijeme sporije teče", kaže Tippett. „Moj model vremenske mašine koristi zakrivljenost prostor-vremena zbog čega je u tom slučaju za putnika vrijeme savijeno u krug, a nije prava linija. Taj krug nas vraća unazad." Iako je moguće opisati ovu vrstu vremenske vožnje pomoću matematičke jednačine, Tippett sumnja da će neko ikada uspjeti izgraditi ovakvu mašinu. „H. G. Wells popularizirao je termin „vremenska mašina" i ostavio ljudima u razmišljanje da li bi se moglo i kako bi se obavilo putovanje kroz vrijeme pomoću „mašine ili neke posebne kutije", kaže Tippett. „Iako je matematički izvodivo, još nije moguće izgraditi mašinu za putovanje kroz vrijeme, jer su nam potrebani materijali, tkz. egzotična materija, da bi se savijao prostor-vrijeme kontinuum u mogućim pravcima. Takvi materijali se tek trebaju otkriti." „Proučavanje prostor-vrijeme matematičkog modela je fascinantno i problematično, ali je u isto vrijeme i zabavan način korištenja matematike i fizike", kaže Tippett. „Stručnjaci iz mog polja istražuju mogućnosti matematičkog modela vremenske mašine još od 1949. godine. I ovo moje istraživanje predstavlja novi metod za takvo nešto." |
|   | | kreja
Master


Poruka : 5893
Lokacija : prva lijevo
Učlanjen : 18.12.2021
Raspoloženje : super
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  Ned 16 Okt - 7:10 Ned 16 Okt - 7:10 | |
| Ojlerov identitet, ili neke od formula Pitagorine teoreme rijetko se pominju u istom kontekstu sa najboljim kompozicijama Mocarta, ili slikama Van Goga.
Međutim, za ljude koji vole matematiku, posmatranje lijepe matematičke formule aktivira iste zone u mozgu, kao i posmatranje nekog umjetničkog djela.Matematika, baš kao i umjetnost, izaziva reakciju u nivou prefrontalnog korteksa, kojeg zovemo i "emocionalni mozak".U istraživačkom radu, objavljenom u časopisu Frontiers in Human Neurosciences, se navodi da je 15 matematičara ocijenilo 60 matematičkih formula kao „lijepe“, „neutralne“ ili „ružne“, a zatim su istraživači koristili funkcionalnu magnetnu rezonancu kako bi se uslikala moždana aktivnost matematičara dok su im pokazivali pomenute formule.One koje su bile označene kao najljepše podstakle su aktivnost u prefrontalnom korteksu, tj. u dijelu mozga koji "vidi" ljepotu kao kada stojimo ispred nekog umjetničkog remek djela ili slušamo muziku.Profesor Semir Zeki kaže „Za mnoge od nas matematičke formule djeluju suho i nepristupačno, ali za matematičara jednačina može predstavljati utjelovljenje ljepote. Ljepota formule može proizilaziti iz jednostavnosti, simetrije, elegancije ili izražavanja nepromjenjive istine. Prema Platonu, apstraktni kvalitet matematike izražava krajnji vrhunac ljepote“.  Formule označene kao najljepše bile su Ojlerov identitet i neke od formula Pitagorine teoreme. Ljepota Ojlerove formule je u njenoj jezivoj eleganciji, a sastoji se iz minimalno broja simbola, u kojima su objedinjene kljucne oblasti matematike: e - (realna) analiza, pi - geometrija, trigonometrija, i - algebra, kompleksna analiza i 0,1 - aritmetika. Kao najružnije označeni su beskonačni niz Srinivase Ramanudžana i Koši-Rimanova funkcionalna jednačina. Profesor Zeki navodi da se mnogi dijelovi mozga aktiviraju kada gledamo u neku jednačinu, ali kada matematičar gleda lijepu jednačinu, tada reaguje emocionalni mozak, odnosno prefrontalni korteks, kao da posmatra lijepu sliku ili sluša muziku. Ovi rezulatati dovode do ključnog pitanja u istraživanju estetike, o kojem se raspravlja još iz klasičnog vremena, a to je da li se estetska iskustva mogu kvantificirati. Formule označene kao najljepše bile su Ojlerov identitet i neke od formula Pitagorine teoreme. Ljepota Ojlerove formule je u njenoj jezivoj eleganciji, a sastoji se iz minimalno broja simbola, u kojima su objedinjene kljucne oblasti matematike: e - (realna) analiza, pi - geometrija, trigonometrija, i - algebra, kompleksna analiza i 0,1 - aritmetika. Kao najružnije označeni su beskonačni niz Srinivase Ramanudžana i Koši-Rimanova funkcionalna jednačina. Profesor Zeki navodi da se mnogi dijelovi mozga aktiviraju kada gledamo u neku jednačinu, ali kada matematičar gleda lijepu jednačinu, tada reaguje emocionalni mozak, odnosno prefrontalni korteks, kao da posmatra lijepu sliku ili sluša muziku. Ovi rezulatati dovode do ključnog pitanja u istraživanju estetike, o kojem se raspravlja još iz klasičnog vremena, a to je da li se estetska iskustva mogu kvantificirati. |
|   | | Sponsored content
 |  Naslov: Re: Zanimljivosti iz matematike Naslov: Re: Zanimljivosti iz matematike  | |
| |
|   | | |
Similar topics |  |
|
| Strana 4 od 4 | Idi na stranu :  1, 2, 3, 4 1, 2, 3, 4 | |
| | Dozvole ovog foruma: | Ne možete odgovarati na teme u ovom forumu
| |
| |
| | Ko je trenutno na forumu | Imamo 585 korisnika na forumu: 0 Registrovanih, 0 Skrivenih i 585 Gosta :: 2 Provajderi
Nema
Najviše korisnika na forumu ikad bilo je 930 dana Pet 27 Sep - 15:38
|
| Dvorana slavnih |
Naj Avatar Haossa !

Kreja
|
| Poslanici naj aktivniji nedelje | |
|